2D Vectors
This page has been automatically translated using the Google Translate API services. We are working on improving texts. Thank you for your understanding and patience.
Header
#include <geom2d/v2d.h>
Functions
| V2D | v2d (...) |
| V2Df | v2d_tof (...) |
| V2Dd | v2d_tod (...) |
| void | v2d_tofn (...) |
| void | v2d_todn (...) |
| V2D | v2d_add (...) |
| V2D | v2d_sub (...) |
| V2D | v2d_mul (...) |
| V2D | v2d_from (...) |
| V2D | v2d_mid (...) |
| V2D | v2d_unit (...) |
| V2D | v2d_unit_xy (...) |
| V2D | v2d_perp_pos (...) |
| V2D | v2d_perp_neg (...) |
| V2D | v2d_from_angle (...) |
| bool_t | v2d_norm (...) |
| real | v2d_length (...) |
| real | v2d_sqlength (...) |
| real | v2d_dot (...) |
| real | v2d_dist (...) |
| real | v2d_sqdist (...) |
| real | v2d_angle (...) |
| void | v2d_rotate (...) |
Types and Constants
| V2D | kZERO |
| V2D | kX |
| V2D | kY |
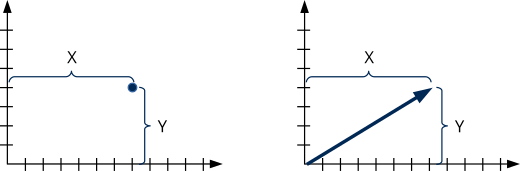
Vector (V2Df, V2Dd) is the most elementary geometric element. It represents a point, a direction or displacement by its two components x and y (Figure 1).
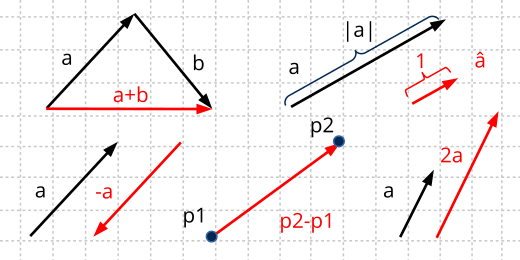
The Vectorial Albegra defines a series of basic operations: Addition, negation, multiplication by a scalar, module and normalization (Formula 1). The visual representation of these operations is in (Figure 2).
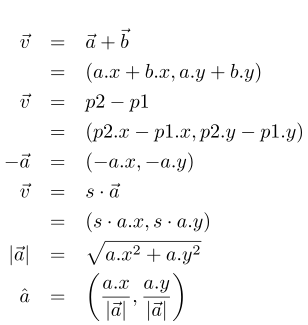
- Use v2d_addf to add two vectors.
- Use v2d_subf to subtract two vectors.
- Use v2d_mulf to multiply by a scalar.
- Use v2d_lengthf to calculate the modulus of a vector.
- Use v2d_normf to normalize a vector.
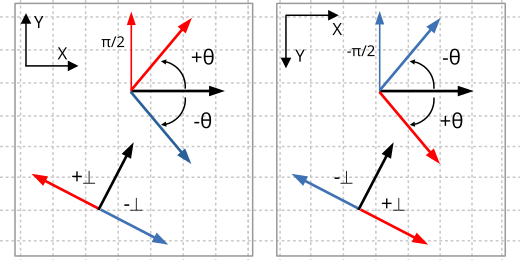
1. CW and CCW angles
The angle of rotation of a vector will always be expressed in radians and the positive direction corresponds to the rotation from the X axis to the Y axis. Normally the counterclockwise direction is associated as positive and the clockwise direction negative. This is true in Cartesian coordinates but not in other types of reference systems, such as images or monitors (Figure 3). We must bear this in mind to avoid confusion, something that happens relatively frequently. The same criterion is applied when calculating the perpendicular vector, differentiating between positive and negative.
- Use v2d_anglef to get the angle between two vectors.
- Use v2d_rotatef to apply a rotation to a vector.
- Use v2d_perp_posf to calculate the positive perpendicular vector.
To avoid confusion, remember that the positive direction is the one that rotates from the X axis to the Y axis. It will be counterclockwise direction in Cartesian coordinates and clockwise direction in screen coordinates.
2. Vector projection
Another operation used quite frequently in geometry is the projection of points onto a vector. Intuitively, we can see it as the point on the vector closest to the original point and that it will always be on the perpendicular line. We will calculate it with the dot product (Formula 2) and its value (scalar) will be the distance from the origin to the projection in the direction of the vector (Figure 4).
- Use v2d_dotf to calculate the dot product of two vectors.
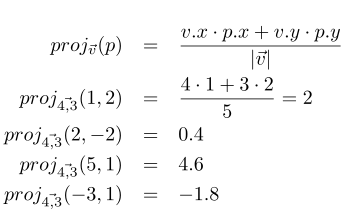
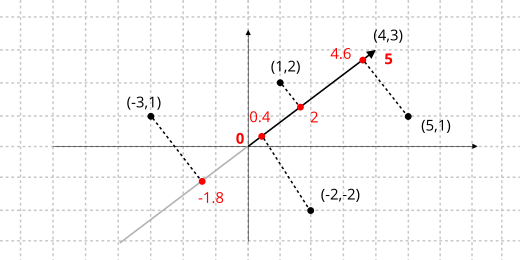
If we are interested in the relative position between different projections, we can avoid dividing by the vector's modulus, which is more computationally efficient by not calculating square roots.
kZERO
const V2Df kV2D_ZEROf; const V2Dd kV2D_ZEROd; const V2D V2D::kZERO;
The (0,0) vector.
kX
const V2Df kV2D_Xf; const V2Dd kV2D_Xd; const V2D V2D::kX;
The (1,0) vector.
kY
const V2Df kV2D_Yf; const V2Dd kV2D_Yd; const V2D V2D::kY;
The (,1) vector.
v2d ()
Create a 2d vector from its components.
V2Df v2df(const real32_t x, const real32_t y); V2Dd v2dd(const real64_t x, const real64_t y); V2D V2D(const real x, const real y);
| x | X coordinate. |
| y | Y coordinate. |
Return
2d vector.
v2d_tof ()
Convert a vector from double to float.
V2Df v2d_tof(const V2Dd *v);
| v | Vector. |
Return
The 2d vector in simple precision.
v2d_tod ()
Convert a vector from float to double.
V2Dd v2d_tod(const V2Df *v);
| v | Vector. |
Return
The 2d vector in double precision.
v2d_tofn ()
Converts a vector array from double to float.
void v2d_tofn(V2Df *vf, const V2Dd *vd, const uint32_t n);
| vf | The destination array. |
| vd | The source array. |
| n | Number of elements. |
v2d_todn ()
Converts a vector array from float to double.
void v2d_todn(V2Dd *vd, const V2Df *vf, const uint32_t n);
| vd | The destination array. |
| vf | The source array. |
| n | Number of elements. |
v2d_add ()
Add two vectors.
V2Df v2d_addf(const V2Df *v1, const V2Df *v2); V2Dd v2d_addd(const V2Dd *v1, const V2Dd *v2); V2D V2D::add(const V2D *v1, const V2D *v2);
| v1 | Vector 1. |
| v2 | Vector 2. |
Return
The result vector.
v2d_sub ()
Subtract two vectors.
V2Df v2d_subf(const V2Df *v1, const V2Df *v2); V2Dd v2d_subd(const V2Dd *v1, const V2Dd *v2); V2D V2D::sub(const V2D *v1, const V2D *v2);
| v1 | Vector 1. |
| v2 | Vector 2. |
Return
The result vector.
v2d_mul ()
Multiply a vector by a scalar.
V2Df v2d_mulf(const V2Df *v, const real32_t s); V2Dd v2d_muld(const V2Dd *v, const real64_t s); V2D V2D::mul(const V2D *v, const real s);
| v | Vector. |
| s | Scalar. |
Return
The result vector.
v2d_from ()
Create a vector from a point and a direction.
V2Df v2d_fromf(const V2Df *v, const V2Df *dir, const real32_t length); V2Dd v2d_fromd(const V2Dd *v, const V2Dd *dir, const real64_t length); V2D V2D::from(const V2D *v, const V2D *dir, const real length);
| v | Initial vector. |
| dir | Direction. |
| length | Length. |
Return
The result vector.
Remarks
It will perform the operation r = v + length * dir. dir does not need to be unitary, in which case length will behave as a scale factor.
v2d_mid ()
Returns the midpoint of two points.
V2Df v2d_midf(const V2Df *v1, const V2Df *v2); V2Dd v2d_midd(const V2Dd *v1, const V2Dd *v2); V2D V2D::mid(const V2D *v1, const V2D *v2);
| v1 | First point. |
| v2 | Second point. |
Return
The middle point.
v2d_unit ()
Unit vector (direction) from 1 to 2.
V2Df v2d_unitf(const V2Df *v1, const V2Df *v2, real32_t *dist); V2Dd v2d_unitd(const V2Dd *v1, const V2Dd *v2, real64_t *dist); V2D V2D::unit(const V2D *v1, const V2D *v2, real *dist);
| v1 | Point 1 (origin). |
| v2 | Point 2 (destination). |
| dist | Distance between points. Can be |
Return
The unit vector.
v2d_unit_xy ()
Unit vector (direction) from 1 to 2.
V2Df v2d_unit_xyf(const real32_t x1, const real32_t y1, const real32_t x2, const real32_t y2, real32_t *dist); V2Dd v2d_unit_xyd(const real64_t x1, const real64_t y1, const real64_t x2, const real64_t y2, real64_t *dist); V2D V2D::unit_xy(const real x1, const real y1, const real x2, const real y2, real *dist);
| x1 | X coordinate of point 1 (origin). |
| y1 | Y coordinate of point 1 (origin). |
| x2 | X coordinate of point 2 (destination). |
| y2 | Y coordinate of point 2 (destination). |
| dist | Distance between points. Can be |
Return
The unit vector.
v2d_perp_pos ()
Gets the positive perpendicular vector.
V2Df v2d_perp_posf(const V2Df *v); V2Dd v2d_perp_posd(const V2Dd *v); V2D V2D::perp_pos(const V2D *v);
| v | Initial vector. |
Return
The perpendicular vector.
Remarks
It is the perpendicular obtained by positive angle (+π/2).
v2d_perp_neg ()
Gets the negative perpendicular vector.
V2Df v2d_perp_negf(const V2Df *v); V2Dd v2d_perp_negd(const V2Dd *v); V2D V2D::perp_neg(const V2D *v);
| v | Initial vector. |
Return
The perpendicular vector.
Remarks
It is the perpendicular obtained by negative angle (-π/2).
v2d_from_angle ()
Gets the vector resulting from applying a rotation to the vector [1,0].
V2Df v2d_from_anglef(const real32_t a); V2Dd v2d_from_angled(const real64_t a); V2D V2D::from_angle(const real a);
| a | Angle. |
Return
The vector.
Remarks
For a=0 we get [1,0]. For a=π/2 [0,1].
v2d_norm ()
Normalize a vector, that is, make it a vector of length = 1.
bool_t v2d_normf(V2Df *v); bool_t v2d_normd(V2Dd *v); bool_t V2D::norm(V2D *v);
| v | Vector that will be normalized. |
Return
FALSE if the vector cannot be normalized (vector 0).
v2d_length ()
Calculate the length of a vector.
real32_t v2d_lengthf(const V2Df *v); real64_t v2d_lengthd(const V2Dd *v); real V2D::length(const V2D *v);
| v | Vector. |
Return
The vector module.
v2d_sqlength ()
Calculate the square of the length of a vector.
real32_t v2d_sqlengthf(const V2Df *v); real64_t v2d_sqlengthd(const V2Dd *v); real V2D::sqlength(const V2D *v);
| v | Vector. |
Return
The square of the vector modulus.
Remarks
Avoid using the square root, so it is more efficient than v2d_lengthf. Often used to compare distances.
v2d_dot ()
Product of two vectors.
real32_t v2d_dotf(const V2Df *v1, const V2Df *v2); real64_t v2d_dotd(const V2Dd *v1, const V2Dd *v2); real V2D::dot(const V2D *v1, const V2D *v2);
| v1 | Vector 1. |
| v2 | Vector 2. |
Return
Scalar product.
v2d_dist ()
Calculate the distance between two points.
real32_t v2d_distf(const V2Df *v1, const V2Df *v2); real64_t v2d_distd(const V2Dd *v1, const V2Dd *v2); real V2D::dist(const V2D *v1, const V2D *v2);
| v1 | The first point. |
| v2 | The second point. |
Return
Distance.
v2d_sqdist ()
Calculate the square of the distance between two points.
real32_t v2d_sqdistf(const V2Df *v1, const V2Df *v2); real64_t v2d_sqdistd(const V2Dd *v1, const V2Dd *v2); real V2D::sqdist(const V2D *v1, const V2D *v2);
| v1 | The first point. |
| v2 | The second point. |
Return
The distance squared.
Remarks
It avoids using the square root, so it is more efficient than v2d_distf. Often used to compare distances.
v2d_angle ()
Calculate the angle formed by two vectors.
real32_t v2d_anglef(const V2Df *v1, const V2Df *v2); real64_t v2d_angled(const V2Dd *v1, const V2Dd *v2); real V2D::angle(const V2D *v1, const V2D *v2);
| v1 | Vector 1. |
| v2 | Vector 2. |
Return
The angle in radians (-Pi, Pi)
Remarks
Positive angles go from v1 to v2 counterclockwise. For angles greater than Pi radians (180°) it will return negative (clockwise).
v2d_rotate ()
Apply a rotation to a vector.
void v2d_rotatef(V2Df *v, const real32_t a); void v2d_rotated(V2Dd *v, const real64_t a); void V2D::rotate(V2D *v, const real a);
| v | Vector to be rotated (origin/destination. |
| a | Angle in radians. |
Remarks
This function involves calculating the sine and cosine. Use t2d_vmultnf if you have to apply the same rotation to multiple vectors.


