Sets
This page has been automatically translated using the Google Translate API services. We are working on improving texts. Thank you for your understanding and patience.
Header
#include <core/setst.h>
Functions
| SetSt(type)* | setst_create (...) |
| void | setst_destroy (...) |
| uint32_t | setst_size (...) |
| type* | setst_get (...) |
| const type* | setst_get_const (...) |
| type* | setst_insert (...) |
| bool_t | setst_delete (...) |
| type* | setst_first (...) |
| const type* | setst_first_const (...) |
| type* | setst_last (...) |
| const type* | setst_last_const (...) |
| type* | setst_next (...) |
| const type* | setst_next_const (...) |
| type* | setst_prev (...) |
| const type* | setst_prev_const (...) |
| void | setst_foreach (...) |
| void | setst_foreach_const (...) |
| void | setst_fornext (...) |
| void | setst_fornext_const (...) |
| void | setst_forback (...) |
| void | setst_forback_const (...) |
| void | setst_forprev (...) |
| void | setst_forprev_const (...) |
The sets are data containers that allow us to work with collections of objects, just like the array. The main difference is that the elements are not stored in contiguous memory locations, but rather use a tree-like structure where each node has two descendants (Figure 1). They are known as BST (binary search trees) or red-black trees.
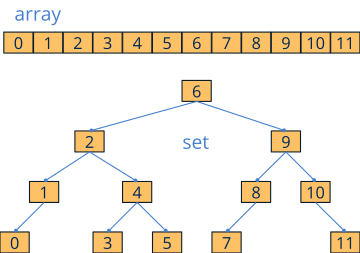
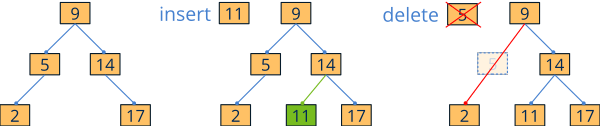
BST are structures optimized for cases where insertions, deletions and searches are very frequent. They are permanently sorted, hence it is possible to insert, delete or locate any element in logarithmic time O(logn), without the need to use sorting functions such as arrst_sort (Figure 2). In order for maintenance to be carried out efficiently, the tree that supports the structure must meet a series of characteristics:
- Binary: Each node can only have 0, 1 or 2 children.
- Ordered: All descendants to the left of a node are of lower value and those to the right of a node are of higher value. The order and search criteria are set in the constructor using a compare-key function and cannot be changed during the lifetime of the container. The new elements will be inserted in their correct position according to this order. It does not support duplicate elements or elements in arbitrary positions.
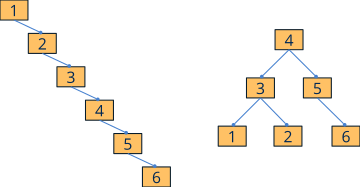
- Balanced: A tree can satisfy both of the above properties, but have degenerated to a list where lookups can no longer be resolved in logarithmic time (Figure 3). Internally, NAppGUI
SetStcontainers are implemented with so-called red-black trees, where a maximum height of2log(n+1)is guaranteed. This is achieved by restructuring the tree after each insertion or deletion, so adding a new element (or deleting it) resolves to a maximum ofO(logn). This is much faster than in arrays, where you have to move all the elements to insert a record in a specific position, with an associated cost ofO(n).
1. Create sets
- Use setst_create to create a set.
- Use setst_destroy to destroy the set and its elements.
Because the set of elements must always remain ordered under the same criteria, we must indicate the object-key comparison function in the constructor (see Comparators and keys) (Listing 1). As occurred when sorting and searching in arrays, we need to define the fields that will make up the unique key of the object, which will allow us to locate elements later. The function that destroys an element of the set should not release the memory occupied by the object itself, since it is managed by the container, just as happens with ArrSt.
char_t* as a key.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 |
typedef struct _product_t Product; struct _product_t { type_t type; String *code; String *desc; Image *image; real32_t price; }; static void i_remove(Product *prod) { str_destroy(&prod->code); str_destroy(&prod->desc); image_destroy(&prod->image); } static int i_compare(const Product *prod, const char_t *code) { return str_cmp(prod->code, code); } SetSt(Product) *products = setst_create(i_compare, Product, char_t); ... setst_destroy(&products, i_remove, Product); |
2. Insert and delete elements in sets
- Use setst_insert to insert an element.
- Use setst_delete to delete an element.
Unlike what happens with arrays, we cannot add elements in any arbitrary position, so inserting implies a search using the object key (Listing 2). If an element with the same key already exists, the insertion will not be carried out and NULL will be returned. Otherwise, we will be returned the memory address where we must initialize our object.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
Product *prod = setst_insert(products, "GTK-1050", Product, char_t); if (prod != NULL) { prod->type = ekHDD; prod->code = str_c("GTK-1050"); prod->desc = str_c("Gigabyte GeForce GTX 1050 OC 2Gb GDDR5"); prod->image = load_image("card.png"); prod->price = 573.34; } else { // Object already exists } ... setst_destroy(&products, i_remove, Product); |
Duplicates are not allowed in SetSt, meaning those elements that have the same key.
Delete is similar to insert, we will only have to provide the key and a destructor. If an element with said key does not exist, FALSE will be returned (Listing 3).
1 2 3 4 5 6 7 8 9 |
bool_t del = setst_delete(products, "GTK-1050", i_remove, Product, char_t); if (del == TRUE) { // Deleted! } else { // Not found } |
3. Search and tour in sets. Iterators
- Use setst_get to search for an element.
- Use setst_next to move the iterator to the next element.
- Use setst_prev to move the iterator to the previous element.
- Use setst_first to move the iterator to the first element of the set.
- Use setst_last to move the iterator to the last element of the set.
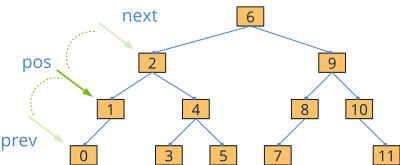
We cannot access the elements of a set using a random index, as was the case with arrays. The nodes are dispersed in different memory areas, which makes it impossible to calculate the position of a specific element from a base address. An iterator is nothing more than a pointer within the set that acts as a marker for the currently selected element (Figure 4). Starting from a specific position, we can move to the previous or next element, but never make arbitrary jumps. In (Listing 4) we see how to go through the elements iterating from the first record, and in (Listing 5) how to locate an element with a known key.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
const Product *prod = setst_first(products, Product); while (prod != NULL) { // Do something ... prod = setst_next(products, Product); } setst_foreach(prod, products, Product) // Do something ... setst_fornext(prod, products, Product) // In reverse order setst_forback(prod, products, Product) // Do something ... setst_forprev(prod, products, Product) |
1 2 3 4 5 6 7 8 9 |
const Product *prod = setst_get_const(products, "GTK-1050", Product, char_t); if (prod != NULL) { // Do something ... // From here, we can move next or prev prod = setst_next(products, Product); } |
After setst_get(), the iterator will be set to the element.
4. Comparison of arrays and sets
(Table 1) shows a performance comparison when using both containers. The Product structure described in (Listing 1) has been used. We will compare six types of containers, combining registers and pointers. The test conditions are:
- Elements will be sorted by the
codefield using thei_comparemethod described in (Listing 1). - Elements have been previously created and reside in memory. The times only reflect the management carried out by the containers.
- The
codefield takes values from"0"to"n-1", wheren=100,000is the number of elements. The elements have been previously shuffled using the bmem_shuffle_n function. - The tests have been carried out on a Raspberry Pi 3 Model B with NAppGUI compiled in Release version. We have chosen this platform due to its clear technical inferiority compared to others. In this way the asymptotic difference is more evident.
| Operation | ArrSt | ArrPt | ArrSt-Sort | ArrPt-Sort | SetSt | SetPt |
| Add(100k) | 0.006 | 0.004 | 27.600 | 2.896 | 0.159 | 0.274 |
| Loop(100k) | 0.000 | 0.000 | 0.000 | 0.000 | 0.022 | 0.025 |
| Search(100k) | 84.139 | 588.080 | 0.101 | 0.218 | 0.121 | 0.232 |
| Sort(100k) | 0.085 | 0.205 | - | - | - | - |
| Delete(100k) | 0.004 | 0.003 | 31.198 | 3.064 | 0.171 | 0.253 |
In view of these data, we can reach the following conclusions:
- Linear searches
O(n)are extremely slow. - Maintaining an ordered array after each insertion or deletion is expensive. It is more efficient to add all the elements and then sort, although this will not always be possible. If the elements enter or leave arbitrarily but the set must always be ordered, it is better to use sets.
- Record-based containers are more efficient in queries, but less efficient in inserting or deleting. However, this test does not include the time to create or free dynamic memory, something inherent to pointer containers.
- Iterating on arrays is practically free, but iterating on sets has a small cost due to the jump logic between nodes.
- We cannot say that one container is better than another in general. It will depend on each specific case.
- For small groups (less than 1000 elements) the differences are practically imperceptible.
- For extremely small groups (up to 100 elements) always use arrays. The asymptotic improvement of sets is clouded by the much more efficient implementation of Arrays.
setst_create ()
Creates an empty set.
SetSt(type)* setst_create(FPtr_compare func_compare, type, ktype);
| func_compare | Function to compare element-key. |
| type | Object type. |
| ktype | Key type. |
Return
The new set.
Remarks
See Create sets.
setst_destroy ()
Destroy a set and all its elements.
void setst_destroy(SetSt(type) **set, FPtr_remove func_remove, type);
| set | The set. It will be set to |
| func_remove | Function that must free the memory associated with the object's fields, but not the object itself. If it is |
| type | Object type. |
setst_size ()
Gets the number of elements in the set.
uint32_t setst_size(const SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Number of elements.
setst_get ()
Searches for an element in O(logn). If it exists, the internal iterator will be set to it.
type* setst_get(SetSt(type) *set, const type *key, type, ktype);
| set | The set. |
| key | Key to search. |
| type | Object type. |
| ktype | Key type. |
Return
Pointer to the element if it exists, or NULL if not.
Remarks
See Search and tour in sets. Iterators.
setst_get_const ()
const version of setst_get.
const type* setst_get_const(const SetSt(type) *set, const type *key, type, ktype);
| set | The set. |
| key | Key. |
| type | Object type. |
| ktype | Key type. |
Return
Element.
setst_insert ()
Inserts a new element into the set.
type* setst_insert(SetSt(type) *set, type *key, type, ktype);
| set | The set. |
| key | Key to insert. |
| type | Object type. |
| ktype | Key type. |
Return
Pointer to the inserted element, which should be used to initialize the object. If an element with the same key already exists, it will return NULL.
Remarks
Inserting or deleting elements overrides the set's internal iterator. You must initialize it again with setst_first or similar. See Insert and delete elements in sets.
setst_delete ()
Removes an element from the set.
bool_t setst_delete(SetSt(type) *set, type *key, FPtr_remove func_remove, type, ktype);
| set | The set. |
| key | Key to delete. |
| func_remove | 'remove' function. |
| type | Object type. |
| ktype | Key type. |
Return
TRUE if the element has been deleted, or FALSE if an element with said key does not exist.
Remarks
Inserting or deleting elements overrides the set's internal iterator. You must initialize it again with setst_first or similar. See Insert and delete elements in sets.
setst_first ()
Gets the first element of the set and initializes the internal iterator.
type* setst_first(SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Pointer to the first element or NULL if the set is empty.
Remarks
See Search and tour in sets. Iterators.
setst_first_const ()
const version of setst_first.
const type* setst_first_const(const SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Element.
setst_last ()
Gets the last element of the set and initializes the internal iterator.
type* setst_last(SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Pointer to the last element or NULL if the set is empty.
Remarks
See Search and tour in sets. Iterators.
setst_last_const ()
const version of setst_last.
const type* setst_last_const(const SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Element.
setst_next ()
Gets the next element of the set, after incrementing the internal iterator.
type* setst_next(SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Pointer to the next element or NULL if the iterator has reached the last one.
Remarks
See Search and tour in sets. Iterators.
setst_next_const ()
const version of setst_next.
const type* setst_next_const(const SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Element.
setst_prev ()
Gets the previous element of the set, after decrementing the internal iterator.
type* setst_prev(SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Pointer to the previous element or NULL if the iterator has reached the first one.
Remarks
See Search and tour in sets. Iterators.
setst_prev_const ()
const version of setst_prev.
const type* setst_prev_const(const SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Element.
setst_foreach ()
Go through all the elements of the set. Use setst_fornext to close the loop.
void setst_foreach(type *elem, SetSt(type) *set, type);
| elem | Name of the 'item' variable inside the loop. |
| set | The set. |
| type | Object type. |
Remarks
See Search and tour in sets. Iterators.
setst_foreach_const ()
const version of setst_foreach.
void setst_foreach_const(const type *elem, const SetSt(type) *set, type);
| elem | Element. |
| set | The set. |
| type | Object type. |
setst_fornext ()
Closes the loop opened by setst_foreach, incrementing the internal iterator.
void setst_fornext(type *elem, SetSt(type) *set, type);
| elem | Name of the variable 'item'. Must be the same as |
| set | The set. |
| type | Object type. |
setst_fornext_const ()
const version of setst_fornext.
void setst_fornext_const(const type *elem, const SetSt(type) *set, type);
| elem | Element. |
| set | The set. |
| type | Object type. |
setst_forback ()
Go through all the elements of the set in reverse order. Use setst_forprev to close the loop.
void setst_forback(const type *elem, type);
| elem | Element. |
| type | Object type. |
Remarks
See Search and tour in sets. Iterators.
setst_forback_const ()
const version of setst_forback.
void setst_forback_const(const type *elem, const SetSt(type) *set, type);
| elem | Element. |
| set | The set. |
| type | Object type. |
setst_forprev ()
Closes the loop opened by setst_forback, decrementing the internal iterator.
void setst_forprev(type *elem, SetSt(type) *set, type);
| elem | Name of the variable 'item'. Must be the same as |
| set | The set. |
| type | Object type. |
setst_forprev_const ()
const version of setst_forprev.
void setst_forprev_const(const type *elem, const SetSt(type) *set, type);
| elem | Element. |
| set | The set. |
| type | Object type. |


