Vectores 2D

Funciones

V2D	v2d (...)
V2Df	v2d_tof (...)
V2Dd	v2d_tod (...)
void	v2d_tofn (...)
void	v2d_todn (...)
V2D	v2d_add (...)
V2D	v2d_sub (...)
V2D	v2d_mul (...)
V2D	v2d_from (...)
V2D	v2d_mid (...)
V2D	v2d_unit (...)
V2D	v2d_unit_xy (...)
V2D	v2d_perp_pos (...)
V2D	v2d_perp_neg (...)
V2D	v2d_from_angle (...)
bool_t	v2d_norm (...)
real	v2d_length (...)
real	v2d_sqlength (...)
real	v2d_dot (...)
real	v2d_dist (...)
real	v2d_sqdist (...)
real	v2d_angle (...)
void	v2d_rotate (...)

Tipos y Constantes

V2D	kZERO
V2D	kX
V2D	kY

1. Ángulos CW y CCW
2. Proyección de vectores

El vector (V2Df, V2Dd) es el elemento geométrico más elemental. Representa un punto, una dirección o un desplazamiento mediante sus dos componentes x e y (Figura 1).

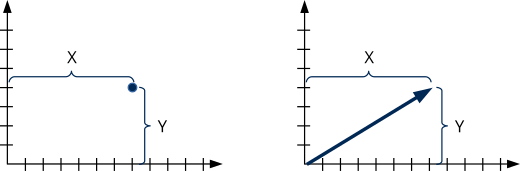
Dibujo de un plano con un punto y un vector. — Figura 1: Un vector 2D representa una posición o un desplazamiento en el plano.

El Álbegra Vectorial define una serie de operaciones básicas: Suma, negación, multiplicación por un escalar, módulo y normalización (Fórmula 1). La representación visual de dichas operaciones la tenemos en (Figura 2).

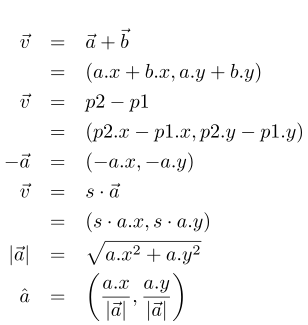
Utiliza v2d_addf para sumar dos vectores.
Utiliza v2d_subf para restar dos vectores.
Utiliza v2d_mulf para multiplicar por un escalar.
Utiliza v2d_lengthf para calcular el módulo de un vector.
Utiliza v2d_normf para normalizar un vector.

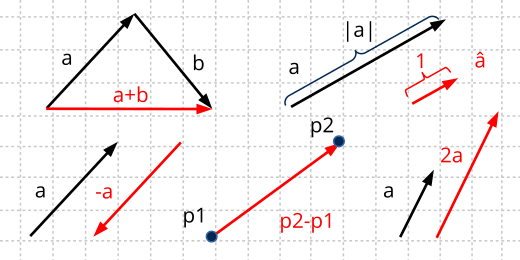
Dibujo de un plano con diferentes operaciones con vectores. — Figura 2: Interpretación geométrica de las operaciones básicas con vectores.

1. Ángulos CW y CCW

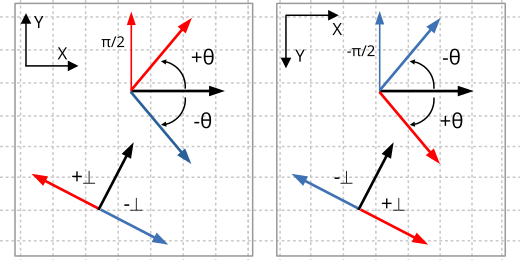
El ángulo de rotación de un vector se expresará siempre en radianes y el sentido positivo corresponde al giro desde el eje X hacia el eje Y. Normalmente se asocia como positiva la dirección antihoraria counter clockwise (CCW) y negativa la dirección horaria clockwise (CW). Esto es cierto en coordenadas cartesianas pero no en otro tipo de sistemas de referencia, como imágenes o monitores (Figura 3). Debemos tenerlo presente para evitar confusiones, algo que sucede con relativa frecuencia. El mismo criterio se aplica al calcular el vector perpendicular, diferenciando entre positivo y negativo.

Utiliza v2d_anglef para obtener el ángulo entre dos vectores.
Utiliza v2d_rotatef para aplicar un giro a un vector.
Utiliza v2d_perp_posf para calcular el vector perpendicular positivo.

Para evitar confusiones recuerda que el sentido positivo es el que gira desde el eje X al eje Y. Será dirección antihoraria en coordenadas cartesianas y dirección horaria en coordenadas de pantalla.

Dibujo de un plano con diferentes rotaciones de vectores. — Figura 3: Rotación de un vector en los sistemas cartesiano y pantalla.

2. Proyección de vectores

Otra operación utilizada con bastante frecuencia en geometría es la proyección de puntos sobre un vector. Intuitivamente, podemos verlo como el punto sobre el vector más cercano al punto original y que siempre estará sobre la línea perpendicular. La calcularemos con el producto escalar (Fórmula 2) y su valor (escalar) será la distancia desde el origen a la proyección en la dirección del vector (Figura 4).

Utiliza v2d_dotf para calcular el producto escalar de dos vectores.

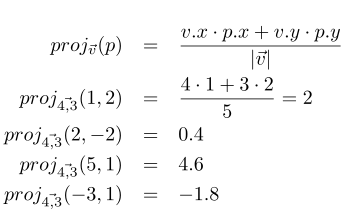
Fórmula 2: Proyección de varios puntos en un vector.

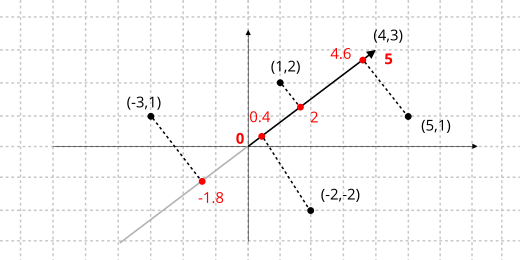
Dibujo de un plano con diferentes proyecciones de puntos en un vector. — Figura 4: Interpretación geométrica de las proyecciones.

Si lo que nos interesa es la posición relativa entre diferentes proyecciones, podemos evitar la división por el módulo del vector, lo que es más eficiente computacionalmente al no calcular raíces cuadradas.

kZERO

const V2Df kV2D_ZEROf;

const V2Dd kV2D_ZEROd;

const V2D V2D::kZERO;

El vector (0,0).

kX

const V2Df kV2D_Xf;

const V2Dd kV2D_Xd;

const V2D V2D::kX;

El vector (1,0).

kY

const V2Df kV2D_Yf;

const V2Dd kV2D_Yd;

const V2D V2D::kY;

El vector (0,1).

v2d ()

Crea un vector 2d a partir de sus componentes.

V2Df
v2df(const real32_t x,
     const real32_t y);

V2Dd
v2dd(const real64_t x,
     const real64_t y);

V2D
V2D(const real x,
    const real y);

x	Coordenada x.
y	Coordenada y.

Retorna

El vector 2d.

v2d_tof ()

Convierte un vector de double a float.

V2Df
v2d_tof(const V2Dd *v);

v	El vector.

Retorna

El vector 2d en simple precisión.

v2d_tod ()

Convierte un vector de float a double.

V2Dd
v2d_tod(const V2Df *v);

v	El vector.

Retorna

El vector 2d en doble precisión.

v2d_tofn ()

Convierte un array de vector de double a float.

void
v2d_tofn(V2Df *vf,
         const V2Dd *vd,
         const uint32_t n);

vf	El array destino.
vd	El array origen.
n	Número de elementos.

v2d_todn ()

Convierte un array de vector de float a double.

void
v2d_todn(V2Dd *vd,
         const V2Df *vf,
         const uint32_t n);

vd	El array destino.
vf	El array origen.
n	Número de elementos.

v2d_add ()

Suma dos vectores.

V2Df
v2d_addf(const V2Df *v1,
         const V2Df *v2);

V2Dd
v2d_addd(const V2Dd *v1,
         const V2Dd *v2);

V2D
V2D::add(const V2D *v1,
         const V2D *v2);

v1	Vector 1.
v2	Vector 2.

Retorna

El vector resultado.

v2d_sub ()

Resta dos vectores.

V2Df
v2d_subf(const V2Df *v1,
         const V2Df *v2);

V2Dd
v2d_subd(const V2Dd *v1,
         const V2Dd *v2);

V2D
V2D::sub(const V2D *v1,
         const V2D *v2);

v1	Vector 1.
v2	Vector 2.

Retorna

El vector resultado.

v2d_mul ()

Multiplica un vector por un escalar.

V2Df
v2d_mulf(const V2Df *v,
         const real32_t s);

V2Dd
v2d_muld(const V2Dd *v,
         const real64_t s);

V2D
V2D::mul(const V2D *v,
         const real s);

v	Vector.
s	Escalar.

Retorna

El vector resultado.

v2d_from ()

Crea un vector a partir de un punto y una dirección.

V2Df
v2d_fromf(const V2Df *v,
          const V2Df *dir,
          const real32_t length);

V2Dd
v2d_fromd(const V2Dd *v,
          const V2Dd *dir,
          const real64_t length);

V2D
V2D::from(const V2D *v,
          const V2D *dir,
          const real length);

v	Vector inicial.
dir	Dirección.
length	Longitud.

Retorna

El vector resultado.

Observaciones

Realizará la operación r = v + length * dir. dir no es necesario que sea unitario, en cuyo caso length se comportará como un factor de escala.

v2d_mid ()

Retorna el punto medio de dos puntos.

V2Df
v2d_midf(const V2Df *v1,
         const V2Df *v2);

V2Dd
v2d_midd(const V2Dd *v1,
         const V2Dd *v2);

V2D
V2D::mid(const V2D *v1,
         const V2D *v2);

v1	Primer punto.
v2	Segundo punto.

Retorna

El punto medio.

v2d_unit ()

Vector unitario (dirección) desde 1 a 2.

V2Df
v2d_unitf(const V2Df *v1,
          const V2Df *v2,
          real32_t *dist);

V2Dd
v2d_unitd(const V2Dd *v1,
          const V2Dd *v2,
          real64_t *dist);

V2D
V2D::unit(const V2D *v1,
          const V2D *v2,
          real *dist);

v1	Punto 1 (origen).
v2	Punto 2 (destino).
dist	Distancia entre puntos. Puede ser `NULL`.

Retorna

El vector unitario.

v2d_unit_xy ()

Vector unitario (dirección) desde 1 a 2.

V2Df
v2d_unit_xyf(const real32_t x1,
             const real32_t y1,
             const real32_t x2,
             const real32_t y2,
             real32_t *dist);

V2Dd
v2d_unit_xyd(const real64_t x1,
             const real64_t y1,
             const real64_t x2,
             const real64_t y2,
             real64_t *dist);

V2D
V2D::unit_xy(const real x1,
             const real y1,
             const real x2,
             const real y2,
             real *dist);

x1	Coordenada X del punto 1 (origen).
y1	Coordenada Y del punto 1 (origen).
x2	Coordenada X del punto 2 (destino).
y2	Coordenada Y del punto 2 (destino).
dist	Distancia entre puntos. Puede ser `NULL`.

Retorna

El vector unitario.

v2d_perp_pos ()

Obtiene el vector perpendicular positivo.

V2Df
v2d_perp_posf(const V2Df *v);

V2Dd
v2d_perp_posd(const V2Dd *v);

V2D
V2D::perp_pos(const V2D *v);

v	Vector inicial.

Retorna

El vector perpendicular.

Observaciones

Es la perpendicular que se obtiene mediante ángulo positivo (+π/2).

v2d_perp_neg ()

Obtiene el vector perpendicular negativo.

V2Df
v2d_perp_negf(const V2Df *v);

V2Dd
v2d_perp_negd(const V2Dd *v);

V2D
V2D::perp_neg(const V2D *v);

v	Vector inicial.

Retorna

El vector perpendicular.

Observaciones

Es la perpendicular que se obtiene mediante ángulo negativo (-π/2).

v2d_from_angle ()

Obtiene el vector resultante de aplicar un giro al vector [1,0].

V2Df
v2d_from_anglef(const real32_t a);

V2Dd
v2d_from_angled(const real64_t a);

V2D
V2D::from_angle(const real a);

Ángulo.

Retorna

El vector.

Observaciones

Para a=0 obtendremos [1,0]. Para a=π/2 [0,1].

v2d_norm ()

Normaliza un vector, es decir, lo convierte en un vector de longitud = 1.

bool_t
v2d_normf(V2Df *v);

bool_t
v2d_normd(V2Dd *v);

bool_t
V2D::norm(V2D *v);

v	El vector que será normalizado.

Retorna

FALSE si el vector no se puede normalizar (el vector 0).

v2d_length ()

Calcula la longitud de un vector.

real32_t
v2d_lengthf(const V2Df *v);

real64_t
v2d_lengthd(const V2Dd *v);

real
V2D::length(const V2D *v);

v	El vector.

Retorna

El módulo del vector.

v2d_sqlength ()

Calcula el cuadrado de la longitud de un vector.

real32_t
v2d_sqlengthf(const V2Df *v);

real64_t
v2d_sqlengthd(const V2Dd *v);

real
V2D::sqlength(const V2D *v);

v	El vector.

Retorna

El cuadrado del módulo del vector.

Observaciones

Evita utilizar la raíz cuadrada, por lo que es más eficiente que v2d_lengthf. Suele utilizarse para comparar distancias.

v2d_dot ()

Producto escalar de dos vectores.

real32_t
v2d_dotf(const V2Df *v1,
         const V2Df *v2);

real64_t
v2d_dotd(const V2Dd *v1,
         const V2Dd *v2);

real
V2D::dot(const V2D *v1,
         const V2D *v2);

v1	Vector 1.
v2	Vector 2.

Retorna

Producto escalar.

v2d_dist ()

Calcula la distancia entre dos puntos.

real32_t
v2d_distf(const V2Df *v1,
          const V2Df *v2);

real64_t
v2d_distd(const V2Dd *v1,
          const V2Dd *v2);

real
V2D::dist(const V2D *v1,
          const V2D *v2);

v1	Punto 1.
v2	Punto 2.

Retorna

La distancia.

v2d_sqdist ()

Calcula el cuadrado de la distancia entre dos puntos.

real32_t
v2d_sqdistf(const V2Df *v1,
            const V2Df *v2);

real64_t
v2d_sqdistd(const V2Dd *v1,
            const V2Dd *v2);

real
V2D::sqdist(const V2D *v1,
            const V2D *v2);

v1	Punto 1.
v2	Punto 2.

Retorna

La distancia al cuadrado.

Observaciones

Evita utilizar la raíz cuadrada, por lo que es más eficiente que v2d_distf. Suele utilizarse para comparar distancias.

v2d_angle ()

Calcula el ángulo formado por dos vectores.

real32_t
v2d_anglef(const V2Df *v1,
           const V2Df *v2);

real64_t
v2d_angled(const V2Dd *v1,
           const V2Dd *v2);

real
V2D::angle(const V2D *v1,
           const V2D *v2);

v1	Vector 1.
v2	Vector 2.

Retorna

El ángulo en radianes (-Pi, Pi)

Observaciones

Los ángulos positivos se expresan desde v1 a v2, en el mismo sentido que el giro del eje X hacia el eje Y. Para ángulos mayores de π rad (180°) se devolverá sentido negativo.

v2d_rotate ()

Aplica un rotación a un vector.

void
v2d_rotatef(V2Df *v,
            const real32_t a);

void
v2d_rotated(V2Dd *v,
            const real64_t a);

void
V2D::rotate(V2D *v,
            const real a);

v	Vector que será rotado (origen/destino).
a	Ángulo en radianes.

Observaciones

Esta función implica calcular el seno y coseno. Utiliza t2d_vmultnf si tienes que aplicar la misma rotación a varios vectores.