2D Polygons
This page has been automatically translated using the Google Translate API services. We are working on improving texts. Thank you for your understanding and patience.
Header
#include <geom2d/pol2d.h>
Functions
| Pol2D* | pol2d_create (...) |
| Pol2D* | pol2d_convex_hull (...) |
| Pol2D* | pol2d_copy (...) |
| void | pol2d_destroy (...) |
| void | pol2d_transform (...) |
| const V2D* | pol2d_points (...) |
| uint32_t | pol2d_n (...) |
| real | pol2d_area (...) |
| Box2D | pol2d_box (...) |
| bool_t | pol2d_ccw (...) |
| bool_t | pol2d_convex (...) |
| V2D | pol2d_centroid (...) |
| V2D | pol2d_visual_center (...) |
| ArrSt(Tri2Df)* | pol2d_triangles (...) |
| ArrSt(Pol2Df)* | pol2d_convex_partition (...) |
Polygons are widely versatile figures, since they allow us to define arbitrary regions delimited by rectilinear segments. Geom2D supports so-called simple polygons, which are those whose sides cannot intersect each other.
- Use pol2d_createf to create a polygon from the path formed by its vertices.
- Use pol2d_ccwf to get the direction of path rotation. See CW and CCW angles.
- Use pol2d_transformf to apply a transformation to the polygon.
- Use pol2d_areaf to get the area.
- Use pol2d_boxf to get the polygon boundaries.
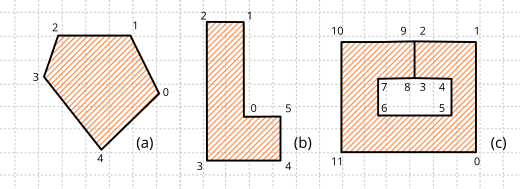
We can classify the polygons into three large groups (Figure 1):
- Convex: The most "desired" from the point of view of calculation simplicity. They are those where any segment that joins two interior points, is totally within the polygon.
- Concave: Or not convex. The opposite of the above. It is one that has an interior angle of more than 180 degrees.
- Weakly: It is one that presents holes through "cut" segments where two vertices are duplicated to allow access and return of each hole. It is an easy way to empty the interior of regions without requiring multiple cycles. The calculation of areas and collisions will take into account these cavities.
1. Polygon center
It is difficult to define a central point in a figure as irregular as a polygon can be. Normally we will interpret as such the centroid or center of mass but, in non-convex cases, this point can be located outside the polygon. In labeling tasks, it is necessary to have a representative point that is within the figure. We consider the visual center to be that point within the polygon located at a maximum distance from any edge (Figure 2). In convex polygons it will coincide with the centroid.
- Use pol2d_centroidf to get the centroid of the polygon.
- Use pol2d_visual_centerf to get the visual center of the polygon. It implements an adaptation of the polylabel algorithm of the MapBox project.

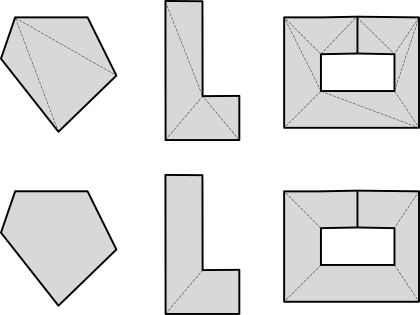
2. Polygon decomposition
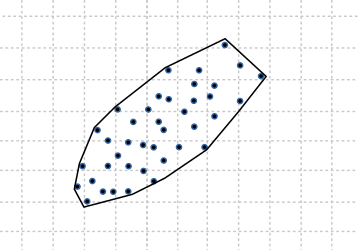
Certain calculations or rendering tasks can be considerably optimized if we reduce the complexity of the geometry to be treated. Decomposing a polygon is nothing more than obtaining a list of simpler polygons whose union is equivalent to the original figure (Figure 3). As an inverse operation, we would have the calculation of the convex hull, which is obtaining the convex polygon that encloses a set of arbitrary points (Figure 4).
- Use pol2d_trianglesf to get a list of the triangles that make up the polygon.
- Use pol2d_convex_partitionf to get a list of convex polygons equivalent to the polygon.
- Use pol2d_convex_hullf to create a convex polygon that "wraps" a set of points.
pol2d_create ()
Create a new polygon.
Pol2Df* pol2d_createf(const V2Df *points, const uint32_t n); Pol2Dd* pol2d_created(const V2Dd *points, const uint32_t n); Pol2D* Pol2D::create(const V2D *points, const uint32_t n);
| points | List of points that make up the polygon. |
| n | Number of points. |
Return
The polygon created.
pol2d_convex_hull ()
Creates the minimum convex polygon that surrounds a set of points (Convex Hull).
Pol2Df* pol2d_convex_hullf(const V2Df *points, const uint32_t n); Pol2Dd* pol2d_convex_hulld(const V2Dd *points, const uint32_t n); Pol2D* Pol2D::convex_hull(const V2D *points, const uint32_t n);
| points | Points list. |
| n | Number of points. |
Return
The polygon.
pol2d_copy ()
Create a copy of the polygon.
Pol2Df* pol2d_copyf(const Pol2Df *pol); Pol2Dd* pol2d_copyd(const Pol2Dd *pol); Pol2D* Pol2D::copy(const Pol2D *pol);
| pol | The original polygon. |
Return
The copy.
pol2d_destroy ()
Destroy the polygon.
void pol2d_destroyf(Pol2Df **pol); void pol2d_destroyd(Pol2Dd **pol); void Pol2D::destroy(Pol2D **pol);
| pol | The polygon. Will be set to |
pol2d_transform ()
Apply a 2D transformation.
void pol2d_transformf(Pol2Df *pol, const T2Df *t2d); void pol2d_transformd(Pol2Dd *pol, const T2Dd *t2d); void Pol2D::transform(Pol2D *pol, const T2D *t2d);
| pol | The polygon. |
| t2d | 2D transformation. |
Remarks
The polygon does not save the original coordinates. Successive transformations will accumulate.
pol2d_points ()
Gets the vertices that make up the polygon.
const V2Df* pol2d_pointsf(const Pol2Df *pol); const V2Dd* pol2d_pointsd(const Pol2Dd *pol); const V2D* Pol2D::points(const Pol2D *pol);
| pol | The polygon. |
Return
Pointer to an array of vertices.
Remarks
Do not modify the returned array. Copy if necessary.
pol2d_n ()
Gets the number of vertices that make up the polygon.
uint32_t pol2d_nf(const Pol2Df *pol); uint32_t pol2d_nd(const Pol2Dd *pol); uint32_t Pol2D::n(const Pol2D *pol);
| pol | The polygon. |
Return
The number of vertices.
Remarks
It is the same value as the one used in the constructor pol2d_createf.
pol2d_area ()
Gets the area of the polygon.
real32_t pol2d_areaf(const Pol2Df *pol); real64_t pol2d_aread(const Pol2Dd *pol); real Pol2D::area(const Pol2D *pol);
| pol | The polygon. |
Return
The area.
pol2d_box ()
Gets the geometric limits of the polygon.
Box2Df pol2d_boxf(const Pol2Df *pol); Box2Dd pol2d_boxd(const Pol2Dd *pol); Box2D Pol2D::box(const Pol2D *pol);
| pol | The polygon. |
Return
Box aligned with the axes, defined by the minimum and maximum vectors.
pol2d_ccw ()
Gets the winding order of the polygon points.
bool_t pol2d_ccwf(const Pol2Df *pol); bool_t pol2d_ccwd(const Pol2Dd *pol); bool_t Pol2D::ccw(const Pol2D *pol);
| pol | The polygon. |
Return
TRUE counter-clockwise. FALSE clockwise.
pol2d_convex ()
Gets whether or not the polygon is convex.
bool_t pol2d_convexf(const Pol2Df *pol); bool_t pol2d_convexd(const Pol2Dd *pol); bool_t Pol2D::convex(const Pol2D *pol);
| pol | The polygon. |
Return
TRUE if is convex. FALSE if no.
pol2d_centroid ()
Gets the centroid (center of mass) of the polygon.
V2Df pol2d_centroidf(const Pol2Df *pol); V2Dd pol2d_centroidd(const Pol2Dd *pol); V2D Pol2D::centroid(const Pol2D *pol);
| pol | The polygon. |
Return
Center of mass.
pol2d_visual_center ()
Gets the visual center or label point.
V2Df pol2d_visual_centerf(const Pol2Df *pol); V2Dd pol2d_visual_centerd(const Pol2Dd *pol); V2D Pol2D::visual_center(const Pol2D *pol);
| pol | The polygon. |
Return
The labeling center.
Remarks
It corresponds to a point within the polygon located at a maximum distance from any edge. In convex polygons it will coincide with the centroid. It implements an adaptation of the polylabel algorithm of the project MapBox.
pol2d_triangles ()
Gets a list of triangles that make up the polygon.
ArrSt(Tri2Df)* pol2d_trianglesf(const Pol2Df *pol); ArrSt(Tri2Df)* pol2d_trianglesd(const Pol2Dd *pol); ArrSt(Tri2Df)* Pol2D::triangles(const Pol2D *pol);
| pol | The polygon. |
Return
Triangle array. Must be destroyed with arrst_destroy(&triangles, NULL, Tri2Df).
Remarks
The union of all the triangles corresponds to the original polygon.
pol2d_convex_partition ()
Gets a list of the convex polygons that make up the polygon.
ArrSt(Pol2Df)* pol2d_convex_partitionf(const Pol2Df *pol); ArrSt(Pol2Df)* pol2d_convex_partitiond(const Pol2Dd *pol); ArrSt(Pol2Df)* Pol2D::convex_partition(const Pol2D *pol);
| pol | The polygon. |
Return
Array of convex polygons. It must be destroyed with arrst_destroy(&polys, pol2d_destroyf, Pol2Df).
Remarks
The union of all polygons corresponds to the original polygon.


