Polígonos 2D

Funciones

Pol2D*	pol2d_create (...)
Pol2D*	pol2d_convex_hull (...)
Pol2D*	pol2d_copy (...)
void	pol2d_destroy (...)
void	pol2d_transform (...)
const V2D*	pol2d_points (...)
uint32_t	pol2d_n (...)
real	pol2d_area (...)
Box2D	pol2d_box (...)
bool_t	pol2d_ccw (...)
bool_t	pol2d_convex (...)
V2D	pol2d_centroid (...)
V2D	pol2d_visual_center (...)
ArrSt(Tri2Df)*	pol2d_triangles (...)
ArrSt(Pol2Df)*	pol2d_convex_partition (...)

1. Centro del polígono
2. Descomposición de polígonos

Los polígonos son figuras ampliamente versátiles, ya que nos permiten definir regiones arbitrarias delimitadas por segmentos rectilíneos. Geom2D soporta los llamados polígonos simples, que son aquellos cuyos lados no pueden intersectar entre sí.

Utiliza pol2d_createf para crear un polígono a partir del recorrido que forman sus vértices.
Utiliza pol2d_ccwf para obtener el sentido de giro del recorrido. Ver Ángulos CW y CCW.
Utiliza pol2d_transformf para aplicar una transformación al polígono.
Utiliza pol2d_areaf para obtener el área.
Utiliza pol2d_boxf para obtener los límites del polígono.

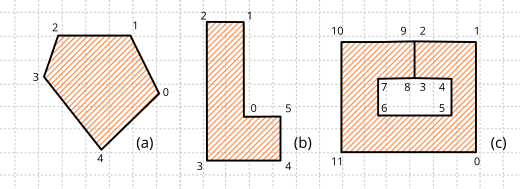
Podemos clasificar a los polígonos en tres grandes grupos (Figura 1):

Convexos: Los más "deseados" desde el punto de vista de la simplicidad de cálculo. Son aquellos donde cualquier segmento que una dos puntos interiores, queda totalmente dentro del polígono.
Cóncavos: O no convexos. Lo opuesto a lo anterior. Es aquel que tiene un ángulo interior de más de 180 grados.
Débiles (Weakly): Es aquel que presenta agujeros por medio de segmentos "de corte" donde dos vértices son duplicados para permitir el acceso y regreso de cada agujero. Es una forma sencilla de vaciar el interior de regiones sin que sean necesarios múltiples ciclos. El cálculo de áreas y colisiones tendrán en cuenta estas cavidades.

Dibujo de varios polígonos en el plano. — Figura 1: Polígonos 2D. (a) Convexo, (b) Cóncavo, (c) Débil. Todos ellos definidos en sentido antihorario *(counter-clockwise)*.

1. Centro del polígono

Es complicado definir un punto central en una figura tan irregular como puede llegar a ser un polígono. Normalmente interpretaremos como tal el centroide o centro de masas pero, en casos no cónvexos, este punto puede localizarse en el exterior del polígono. En tareas de etiquetado se hace necesario disponer de un punto representativo que esté dentro de la figura. Consideramos como centro visual a aquel punto dentro del polígono situado a una distancia máxima de cualquier borde (Figura 2). En polígonos convexos coincidirá con el centroide.

Utiliza pol2d_centroidf para obtener el centroide del polígono.
Utiliza pol2d_visual_centerf para obtener el centro visual del polígono. Implementa una adaptación del algoritmo polylabel del proyecto MapBox.

Puntos centrales de polígonos irregulares. — Figura 2: Punto "central" de un polígono. Línea: Centroide, Relleno: Centro visual o de etiquetado.

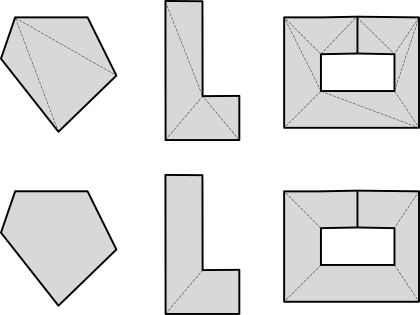
2. Descomposición de polígonos

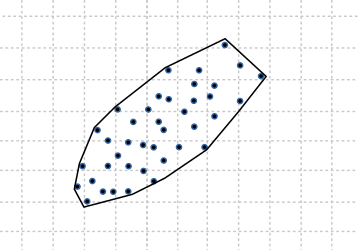
Determinados cálculos o tareas de renderizado se pueden optimizar considerablemente si reducimos la complejidad de la geometría a tratar. Descomponer un polígono no es más que obtener una lista de polígonos más simples cuya unión equivale a la figura original (Figura 3). Como operación inversa, tendríamos el cálculo de la envoltura convexa Convex Hull, que es la obtención del polígono convexo que encierra a un conjunto de puntos arbitrarios (Figura 4).

Utiliza pol2d_trianglesf para obtener una lista de los triángulos que forman el polígono.
Utiliza pol2d_convex_partitionf para obtener una lista polígonos convexos equivalentes al polígono.
Utiliza pol2d_convex_hullf para crear un polígono convexo que "envuelva" a un conjunto de puntos.

Ejemplo de triangulación de polígonos y sub-polígonos convexos. — Figura 3: Descomposición de un polígono mediante triangulación o componentes convexas.

Representación de la envoltura convexa. — Figura 4: Envoltura convexa de un conjunto de puntos.

pol2d_create ()

Crea un nuevo polígono.

Pol2Df*
pol2d_createf(const V2Df *points,
              const uint32_t n);

Pol2Dd*
pol2d_created(const V2Dd *points,
              const uint32_t n);

Pol2D*
Pol2D::create(const V2D *points,
              const uint32_t n);

points	Lista de puntos que forman el polígono.
n	Número de puntos.

Retorna

El polígono creado.

pol2d_convex_hull ()

Crea el polígono convexo mínimo que envuelve a un conjunto de puntos (Convex Hull).

Pol2Df*
pol2d_convex_hullf(const V2Df *points,
                   const uint32_t n);

Pol2Dd*
pol2d_convex_hulld(const V2Dd *points,
                   const uint32_t n);

Pol2D*
Pol2D::convex_hull(const V2D *points,
                   const uint32_t n);

points	Lista de puntos.
n	Número de puntos.

Retorna

El polígono.

pol2d_copy ()

Crea una copia del polígono.

Pol2Df*
pol2d_copyf(const Pol2Df *pol);

Pol2Dd*
pol2d_copyd(const Pol2Dd *pol);

Pol2D*
Pol2D::copy(const Pol2D *pol);

pol	El polígono original.

Retorna

El polígono copiado.

pol2d_destroy ()

Destruye el polígono.

void
pol2d_destroyf(Pol2Df **pol);

void
pol2d_destroyd(Pol2Dd **pol);

void
Pol2D::destroy(Pol2D **pol);

pol	El polígono. Será puesto a `NULL` tras la destrucción.

pol2d_transform ()

Aplica una transformación 2D.

void
pol2d_transformf(Pol2Df *pol,
                 const T2Df *t2d);

void
pol2d_transformd(Pol2Dd *pol,
                 const T2Dd *t2d);

void
Pol2D::transform(Pol2D *pol,
                 const T2D *t2d);

pol	El polígono.
t2d	Transformación 2D.

Observaciones

El polígono no guarda las coordenadas originales. Sucesivas transformaciones se irán acumulando.

pol2d_points ()

Obtiene los vértices que forman el polígono.

const V2Df*
pol2d_pointsf(const Pol2Df *pol);

const V2Dd*
pol2d_pointsd(const Pol2Dd *pol);

const V2D*
Pol2D::points(const Pol2D *pol);

pol	El polígono.

Retorna

Puntero a un array de vértices.

Observaciones

No modificar el array devuelto. Copiar si fuera necesario.

pol2d_n ()

Obtiene el número de vértices que forman el polígono.

uint32_t
pol2d_nf(const Pol2Df *pol);

uint32_t
pol2d_nd(const Pol2Dd *pol);

uint32_t
Pol2D::n(const Pol2D *pol);

pol	El polígono.

Retorna

El número de vértices.

Observaciones

Es el mismo valor que el utilizado en el constructor pol2d_createf.

pol2d_area ()

Obtiene el área del polígono.

real32_t
pol2d_areaf(const Pol2Df *pol);

real64_t
pol2d_aread(const Pol2Dd *pol);

real
Pol2D::area(const Pol2D *pol);

pol	El polígono.

Retorna

El área.

pol2d_box ()

Obtiene los límites geométricos del polígono.

Box2Df
pol2d_boxf(const Pol2Df *pol);

Box2Dd
pol2d_boxd(const Pol2Dd *pol);

Box2D
Pol2D::box(const Pol2D *pol);

pol	El polígono.

Retorna

Caja alineada con los ejes, definida por los vectores mínimo y máximo.

pol2d_ccw ()

Obtiene el orden del recorrido de los puntos del polígono.

bool_t
pol2d_ccwf(const Pol2Df *pol);

bool_t
pol2d_ccwd(const Pol2Dd *pol);

bool_t
Pol2D::ccw(const Pol2D *pol);

pol	El polígono.

Retorna

TRUE sentido antihorario counter-clockwise. FALSE sentido horario clockwise.

pol2d_convex ()

Obtiene si el polígono es o no convexo.

bool_t
pol2d_convexf(const Pol2Df *pol);

bool_t
pol2d_convexd(const Pol2Dd *pol);

bool_t
Pol2D::convex(const Pol2D *pol);

pol	El polígono.

Retorna

TRUE si es convexo. FALSE si no.

pol2d_centroid ()

Obtiene el centroide (centro de masas) del polígono.

V2Df
pol2d_centroidf(const Pol2Df *pol);

V2Dd
pol2d_centroidd(const Pol2Dd *pol);

V2D
Pol2D::centroid(const Pol2D *pol);

pol	El polígono.

Retorna

El centro de masas.

pol2d_visual_center ()

Obtiene el centro visual o punto de etiquetado.

V2Df
pol2d_visual_centerf(const Pol2Df *pol);

V2Dd
pol2d_visual_centerd(const Pol2Dd *pol);

V2D
Pol2D::visual_center(const Pol2D *pol);

pol	El polígono.

Retorna

El centro de etiquetado.

Observaciones

Corresponde a un punto dentro del polígono situado a una distancia máxima de cualquier borde. En polígonos convexos coincidirá con el centroide. Implementa una adaptación del algoritmo polylabel del proyecto MapBox.

pol2d_triangles ()

Obtiene una lista de triángulos que forman el polígono.

ArrSt(Tri2Df)*
pol2d_trianglesf(const Pol2Df *pol);

ArrSt(Tri2Df)*
pol2d_trianglesd(const Pol2Dd *pol);

ArrSt(Tri2Df)*
Pol2D::triangles(const Pol2D *pol);

pol	El polígono.

Retorna

Array de triángulos. Debe ser destruido con arrst_destroy(&triangles, NULL, Tri2Df).

Observaciones

La unión de todos los triángulos corresponde con el polígono original.

pol2d_convex_partition ()

Obtiene una lista de los polígonos convexos que forman el polígono.

ArrSt(Pol2Df)*
pol2d_convex_partitionf(const Pol2Df *pol);

ArrSt(Pol2Df)*
pol2d_convex_partitiond(const Pol2Dd *pol);

ArrSt(Pol2Df)*
Pol2D::convex_partition(const Pol2D *pol);

pol	El polígono.

Retorna

Array de polígonos convexos. Debe ser destruido con arrst_destroy(&polys, pol2d_destroyf, Pol2Df).

Observaciones

La unión de todos los polígonos corresponde con el polígono original.