Transformaciones 2D
Cabecera
#include <geom2d/t2d.h>
Funciones
| void | t2d_tof (...) |
| void | t2d_tod (...) |
| void | t2d_move (...) |
| void | t2d_rotate (...) |
| void | t2d_scale (...) |
| void | t2d_invfast (...) |
| void | t2d_inverse (...) |
| void | t2d_mult (...) |
| void | t2d_vmult (...) |
| void | t2d_vmultn (...) |
| void | t2d_decompose (...) |
Tipos y Constantes
| T2D | kIDENT |
Las transformaciones afines son operaciones matemáticas que permiten realizar cambios de coordenadas entre diferentes sistemas de referencia. Por ejemplo, en (Figura 1) (a) construimos un polígono expresando las coordenadas de sus vértices en un sistema cartesiano: [ (4,1), (2,5), (-3,5), (-4,2), (0,-3) ]. Ahora imaginemos que queremos dibujar varias instancias del mismo en un plano, cada una de ellas con diferente posición, orientación y tamaño (Figura 1) (b). Necesitaríamos calcular las coordenadas de los puntos del polígono original en las nuevas ubicaciones, con el fin de trazar correctamente las líneas que delimitan cada copia.
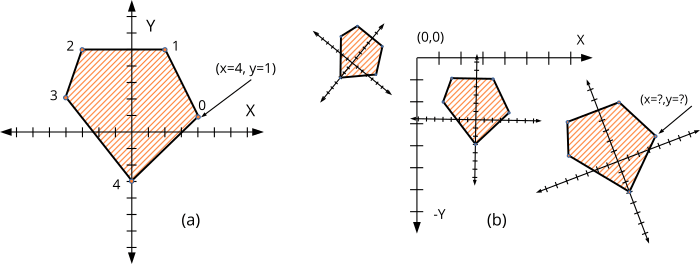
El Álgebra Vectorial nos brinda una poderosa herramienta con la que se puede expresar la relación entre dos sistemas utilizando seis número reales (Figura 2). Los primeros cuatro valores corresponden a una matriz 2x2 con las coordenadas de los vectores X=[1,0] e Y=[0,1] del nuevo sistema de referencia. Esta matriz integra una posible rotación y escalado de los ejes. Los últimos dos valores indican un desplazamiento del origen. En (Fórmula 1) tenemos el desarrollo matemático para transformar el punto [4,1] a una nueva base girada 25° con respecto al origen y desplazada 11 unidades en el eje X y -5 en el eje Y. Aplicando la misma operación a cada punto, transformaríamos el objeto completo.
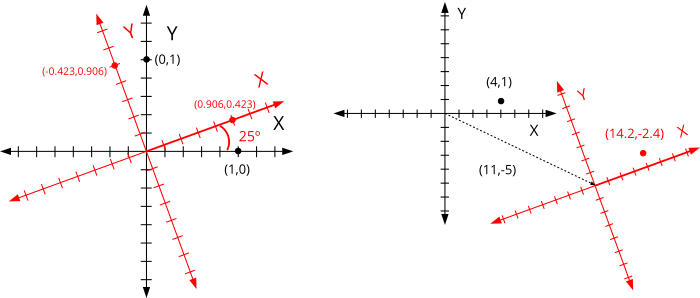
![Transformación del punto [4,1].](../../img/geom2d/aplin.png)
1. Clasificación de transformaciones
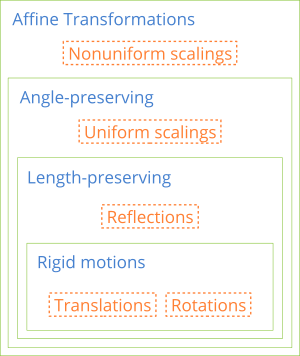
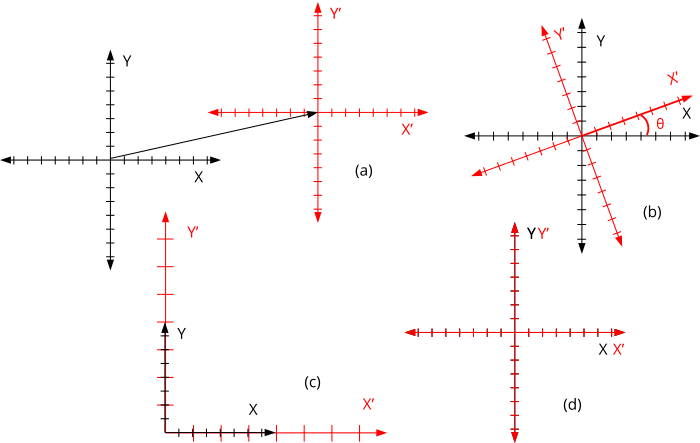
En principio, cualquier combinación de valores [i.x, i.y, j.x, j.y, p.x, p.y] proporcionaría una transformación válida, aunque si no los elegimos con cierto criterio obtendremos aberraciones poco útiles en la práctica. Las transformaciones más utilizadas en aplicaciones gráficas y de ingeniería son (Figura 3) (Figura 4) (Fórmula 2):
- Traslación (a): Desplaza el origen del objeto a otro punto.
- Rotación (b): Gira el objeto sobre el origen de su sistema local.
- Escalado (c): Cambia el tamaño. Si sx < 1, reduce. sx > 1, aumenta. sx = 1, no varía. En escalados no uniformes, sx y sy tienen valores diferentes, lo que producirá una deformación en la relación de aspecto.
- Identidad (d): Es la transformación nula. Al aplicarla, los vectores permanecen inalterados.
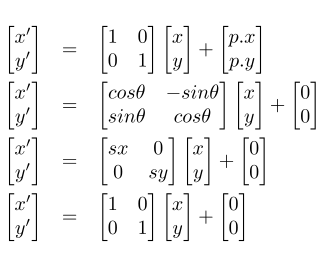
2. Composición de transformaciones
Es posible componer o acumular transformaciones mediante la multiplicación de matrices (Fórmula 3). Lo habitual en modelos 2d será obtener la ubicación final de un objeto a partir de las transformaciones elementales traslación, rotación y escalado. La acumulación también es útil para posicionar elementos en estructuras jerárquicas, donde la ubicación de cada objeto depende directamente de la de su nodo superior (padre).
- Utiliza t2d_movef para acumular un desplazamiento a una transformación existente.
- Utiliza t2d_rotatef para acumular una rotación.
- Utiliza t2d_scalef para acumular un escalado.
- Utiliza t2d_multf para acumular una transformación a otra ya existente.
- Utiliza t2d_vmultf para aplicar una transformación a un vector.
- Utiliza t2d_vmultnf para aplicar una transformación a varios vectores.
- Utiliza kT2D_IDENTf para hacer referencia a la transformación identidad.
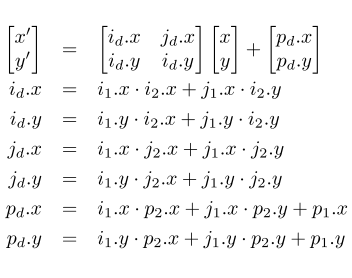
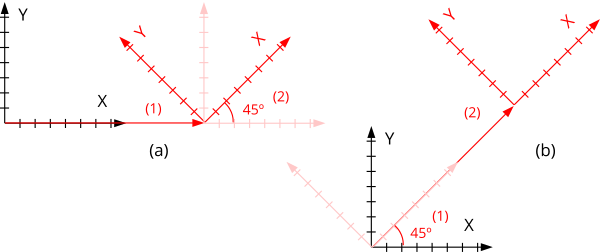
La multiplicación matricial no es conmutativa, si no que el orden en el que se apliquen las operaciones afectará al resultado final. Por ejemplo, en (Figura 5) (a), se ha trasladado el origen y después aplicado una rotación. En (Figura 5) (b) se ha hecho al contrario, primero rotar y luego trasladar.
1 2 3 4 5 6 7 8 9 |
// (a) First move, then rotate T2Df t2d; t2d_movef(&t2d, kT2D_IDENTf, 11, 0); t2d_rotatef(&t2d, &t2d, kBMATH_PIf / 4); // (b) First rotate, then move T2Df t2d; t2d_rotatef(&t2d, kT2D_IDENTf, kBMATH_PIf / 4); t2d_movef(&t2d, &t2d, 11, 0); |
3. Descomposición e inversa
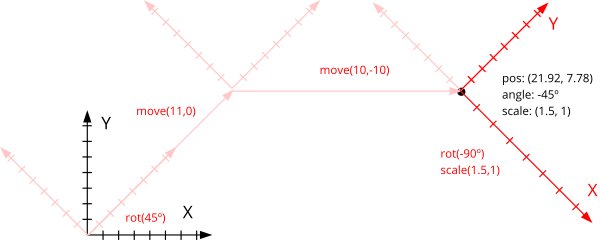
Cualquier cadena de traslaciones, rotaciones y escalados define un sistema de referencia afín que puede ser expresado en función de un único desplazamiento, rotación y escalado (Figura 6). Podemos "deshacer" dicha transformación y volver al origen mediante la transformación inversa (Listado 2).
- Utiliza t2d_decomposef para obtener las componentes de una transformación.
- Utiliza t2d_inversef para obtener la transformación inversa.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
T2Df t2d, inv, inv2; V2Df pos, sc; real32_t a; // Transform sequence t2d_rotatef(&t2d, kT2D_IDENTf, kBMATH_PIf / 4); t2d_movef(&t2d, &t2d, 11, 0); t2d_movef(&t2d, &t2d, 10, - 10); t2d_rotatef(&t2d, &t2d, - kBMATH_PIf / 2); t2d_scalef(&t2d, &t2d, 1.5f, 1); // Transform components t2d_decomposef(&t2d, &pos, &a, &sc); // Transform inverse t2d_inversef(&inv, &t2d); // Inverse from components t2d_scalef(&inv2, kT2D_IDENTf, 1/sc.x, 1/sc.y); t2d_rotatef(&inv2, &inv2, -a); t2d_movef(&inv2, &inv2, -pos.x, -pos.y); // inv == inv2 ('inv' more numerical accurate) |
kIDENT
const T2Df kT2D_IDENTf; const T2Dd kT2D_IDENTd; const T2D T2D::kIDENT;
Representa la transformación identidad.
t2d_tof ()
Convierte una transformación de double a float.
void t2d_tof(T2Df *dest, const T2Dd *src);
| dest | Transformación destino. |
| src | Transformación origen. |
t2d_tod ()
Convierte una transformación de float a double.
void t2d_tod(T2Dd *dest, const T2Df *src);
| dest | Transformación destino. |
| src | Transformación origen. |
t2d_move ()
Multiplica una transformación por una traslación dest = src * move(x,y).
void t2d_movef(T2Df *dest, const T2Df *src, const real32_t x, const real32_t y); void t2d_moved(T2Dd *dest, const T2Dd *src, const real64_t x, const real64_t y); void T2D::move(T2D *dest, const T2D *src, const real x, const real y);
| dest | Transformación resultado. |
| src | Transformación inicial. |
| x | Coordenada x del desplazamiento. |
| y | Coordenada y del desplazamiento. |
Observaciones
dest y src pueden apuntar a la misma matrix.
t2d_rotate ()
Multiplica una transformación por una rotación dest = src * rotate(a).
void t2d_rotatef(T2Df *dest, const T2Df *src, const real32_t a); void t2d_rotated(T2Dd *dest, const T2Dd *src, const real64_t a); void T2D::rotate(T2D *dest, const T2D *src, const real a);
| dest | Transformación resultado. |
| src | Transformación inicial. |
| a | Ángulo de rotación en radianes. Los ángulos positivos son los que giran desde el eje X al eje Y. |
Observaciones
dest y src pueden apuntar a la misma matrix.
t2d_scale ()
Multiplica una transformación por un escalado dest = src * scale(sx,sy).
void t2d_scalef(T2Df *dest, const T2Df *src, const real32_t sx, const real32_t sy); void t2d_scaled(T2Dd *dest, const T2Dd *src, const real64_t sx, const real64_t sy); void T2D::scale(T2D *dest, const T2D *src, const real sx, const real sy);
| dest | Transformación resultado. |
| src | Transformación inicial. |
| sx | Escalado en el eje x. |
| sy | Escalado en el eje y. |
Observaciones
dest y src pueden apuntar a la misma matrix.
t2d_invfast ()
Calcula la transformación inversa, suponiendo que la entrada sea ortogonal.
void t2d_invfastf(T2Df *dest, const T2Df *src); void t2d_invfastd(T2Dd *dest, const T2Dd *src); void T2D::invfast(T2D *dest, const T2D *src);
| dest | Transformación inversa. |
| src | Transformación inicial. |
Observaciones
La transformación será ortogonal solo si contiene rotaciones y traslaciones, de lo contrario el resultado de aplicarla será impredecible. dest y src pueden apuntar a la misma matrix.
t2d_inverse ()
Calcula la transformación inversa.
void t2d_inversef(T2Df *dest, const T2Df *src); void t2d_inversed(T2Dd *dest, const T2Dd *src); void T2D::inverse(T2D *dest, const T2D *src);
| dest | Transformación inversa. |
| src | Transformación inicial. |
Observaciones
dest y src pueden apuntar a la misma matriz.
t2d_mult ()
Multiplica dos transformaciones dest = src1 * src2.
void t2d_multf(T2Df *dest, const T2Df *src1, const T2Df *src2); void t2d_multd(T2Dd *dest, const T2Dd *src1, const T2Dd *src2); void T2D::mult(T2D *dest, const T2D *src1, const T2D *src2);
| dest | Transformación resultado. |
| src1 | Primer operando. |
| src2 | Segundo operando. |
Observaciones
dest, src1 y src2 pueden apuntar a la misma matrix.
t2d_vmult ()
Transforma un vector dest = t2d * src.
void t2d_vmultf(V2Df *dest, const T2Df *t2d, const V2Df *src); void t2d_vmultd(V2Dd *dest, const T2Dd *t2d, const V2Dd *src); void T2D::vmult(V2D *dest, const T2D *t2d, const V2D *src);
| dest | Vector transformado. |
| t2d | Transformación. |
| src | Vector original. |
Observaciones
dest y src pueden apuntar al mismo vector.
t2d_vmultn ()
Transforma una lista de vectores dest[i] = t2d * src[i].
void t2d_vmultnf(V2Df *dest, const T2Df *t2d, const V2Df *src, const uint32_t n); void t2d_vmultnd(V2Dd *dest, const T2Dd *t2d, const V2Dd *src, const uint32_t n); void T2D::vmultn(V2D *dest, const T2D *t2d, const V2D *src, const uint32_t n);
| dest | Array de vectores transformado. |
| t2d | Transformación. |
| src | Array de vectores original. |
| n | Número de vectores en |
Observaciones
dest y src pueden apuntar al mismo array.
t2d_decompose ()
Obtiene la posición, rotación y escalado de una transformación.
void t2d_decomposef(const T2Df *t2d, V2Df *pos, real32_t *a, V2Df *sc); void t2d_decomposed(const T2Dd *t2d, V2Dd *pos, real64_t *a, V2Dd *sc); void T2D::decompose(const T2D *t2d, V2D *pos, real *a, V2D *sc);
| t2d | Transformación. |
| pos | Posición. Puede ser |
| a | Ángulo en radianes (-π/2, π/2). Puede ser |
| sc | Escalado. Puede ser |
Observaciones
Si la transformación no está compuesta por una secuencia de traslaciones, rotaciones y escalados, el resultado no será válido.


