Contextos 2D
Cabecera
#include <draw2d/dctx.h>
Funciones
| DCtx* | dctx_bitmap (...) |
| Image* | dctx_image (...) |
| void | draw_clear (...) |
| void | draw_matrix (...) |
| void | draw_matrix_cartesian (...) |
| void | draw_antialias (...) |
Los gráficos vectoriales se componen a base de primitivas básicas tales como líneas, círculos, texto, etc, utilizando el algoritmo del pintor (Figura 1): Las operaciones entrantes se superponen o solapan a las ya existentes. El resultado se va almacenando en un búfer intermedio conocido como canvas o surface. Esta superficie de dibujo forma parte de un objeto denominado contexto que también mantiene ciertos parámetros relacionados con el aspecto de las primitivas: Colores, atributos de línea, sistema de referencia, gradientes, etc.
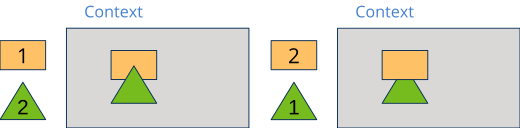
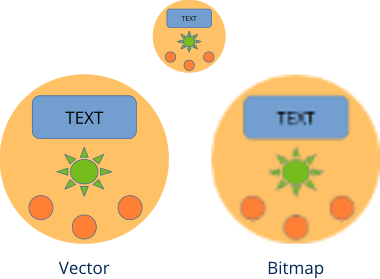
Una de las ventajas de trabajar con formas paramétricas, es que pueden realizarse escalados de la imagen sin perdida de calidad (Figura 2). Esto es debido a que la conversión a píxeles, proceso denominado rasterización (Figura 3), se realiza en tiempo real y se ajusta constantemente al cambio de los vectores. En imágenes bitmap, un aumento de tamaño tiene asociada una pérdida de calidad.

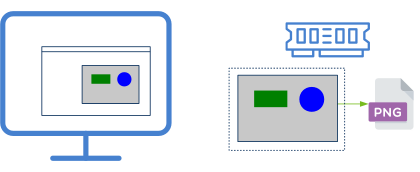
Draw2D permite trabajar con dos tipos de contextos (Figura 4).
- Contexto ventana. El destino será un área dentro de la interfaz de usuario gestionada por un control View. Este control mantiene su propio contexto de dibujo y lo envía "listo para usar" a través del evento EvDraw (Listado 1).
- Contexto imagen. Aquí los comandos de dibujo se volcarán directamente en memoria para, posteriormente, obtener una imagen con el resultado final (Listado 2).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
static void i_OnDraw(App *app, Event *e) { const EvDraw *p = event_params(e, EvDraw); draw_clear(p->ctx, color_rgb(200, 200, 200)); draw_fill_color(p->ctx, color_rgb(0, 128, 0)); draw_rect(p->ctx, ekFILL, 100, 100, 200, 100); draw_fill_color(p->ctx, color_rgb(0, 0, 255)); draw_circle(p->ctx, ekFILL, 450, 150, 75); } View *view = view_create(); view_size(view, s2df(600, 400)); view_OnDraw(view, listener(app, i_OnDraw, App)); |
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
static i_draw(void) { Image *image = NULL; DCtx *ctx = dctx_bitmap(600, 400, ekRGBA32); draw_clear(ctx, color_rgb(200, 200, 200)); draw_fill_color(ctx, color_rgb(0, 128, 0)); draw_rect(ctx, ekFILL, 100, 100, 200, 100); draw_fill_color(ctx, color_rgb(0, 0, 255)); draw_circle(ctx, ekFILL, 450, 150, 75); image = dctx_image(&ctx); image_to_file(image, "drawing.png", NULL); image_destroy(&image); } |
Como podemos observar viendo el código, el dibujo propiamente dicho se realiza de la misma manera, lo único que cambia es como hemos obtenido el contexto (DCtx). Esto permite que podamos escribir rutinas gráficas genéricas sin preocuparnos sobre cual será el destino del resultado final. En el ejemplo DrawImg tienes un desarrollo práctico paso a paso del uso de contextos. Las imágenes que acompañan el resto del capítulo han sido obtenidas de dicha aplicación.
Debido a que no es imperativo disponer de una ventana para dibujar, Draw2d puede utilizarse en aplicaciones de consola para componer o editar imágenes de forma automatizada.
1. Sistemas de referencia
El origen de coordenadas del dibujo se sitúa en la esquina superior izquierda (Figura 5). Las X positivas se desplazan hacia la izquierda y las Y positivas hacia abajo. Las unidades se miden en píxeles (o puntos en Pantallas retina). Por ejemplo, el comando:
1 |
draw_circle(ctx, ekSKFILL, 300, 200, 100); |
dibujará un círculo de 100 píxeles de radio cuyo centro se encuentra a 300 píxeles a la izquierda y 200 píxeles hacia abajo del origen. A este sistema inicial se le denomina identidad ya que todavía no ha sido manipulado, como veremos a continuación.
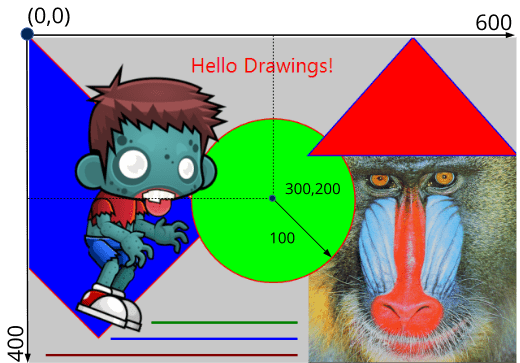
Aunque la escala inicial esté en píxeles, debemos desterrar la idea de que estamos manipulando directamente píxeles al dibujar. Los contextos de dibujo utilizan coordenadas en punto flotante. Por ejemplo, dibujar una línea entre los puntos (0.23, 1.432) y (-45.29, 12.6756) es perfectamente válido. Las transformaciones y el antialiasing pueden alterar ligeramente la posición o el grosor de ciertas líneas. Tampoco debemos esperar resultados "idénticos" a nivel de píxel al migrar las aplicaciones a diferentes plataformas, ya que cada sistema utiliza sus propios algoritmos de rasterización. Debemos pensar que estamos dibujando en el plano real. Para manipular directamente los píxeles de una imagen, consulta Pixel Buffer.
Este sistema de referencia inicial se puede manipular mediante Transformaciones 2D. Las transformaciones más comunes en gráficos son: Traslaciones (Figura 6), Rotaciones (Figura 7) y Escalados (Figura 8).
- draw_matrixf cambiará el sistema de referencia del contexto.
1 2 3 4 |
T2Df t2d; t2d_movef(&t2d, kT2D_IDENTf, 100, 100); draw_matrixf(ctx, &t2d); i_draw(...); |

1 2 3 4 |
T2Df t2d; t2d_rotatef(&t2d, kT2D_IDENTf, 15 * kBMATH_DEG2RADf); draw_matrixf(ctx, &t2d); i_draw(...); |
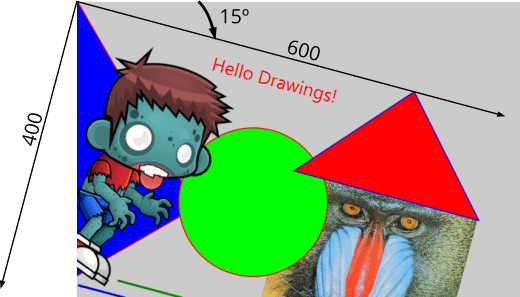
1 2 3 4 |
T2Df t2d; t2d_scalef(&t2d, kT2D_IDENTf, .5f, .5f); draw_matrixf(ctx, &t2d); i_draw(...); |
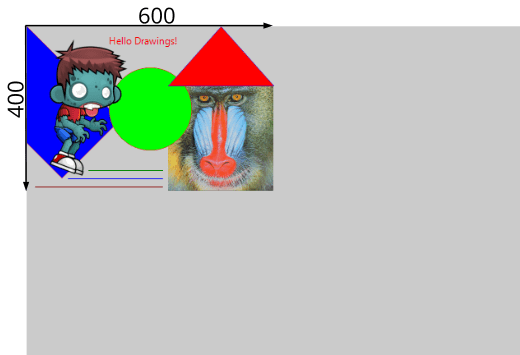
Las transformaciones se pueden acumular, pero debemos tener presente que no son operaciones conmutativas, sino que el orden en que se aplican influirá en el resultado final. Por ejemplo en (Figura 9) observamos que el dibujo se ha desplazado (100, 50) píxeles, en lugar de los (200, 100), debido a que la traslación está afectada por el escalado previo. Más detalles en Composición de transformaciones.
1 2 3 4 5 6 |
T2Df t2d; t2d_scalef(&t2d, kT2D_IDENTf, .5f, .5f); t2d_movef(&t2d, &t2d, 200, 100); t2d_rotatef(&t2d, &t2d, 15 * kBMATH_DEG2RADf); draw_matrixf(ctx, &t2d); i_draw(...); |
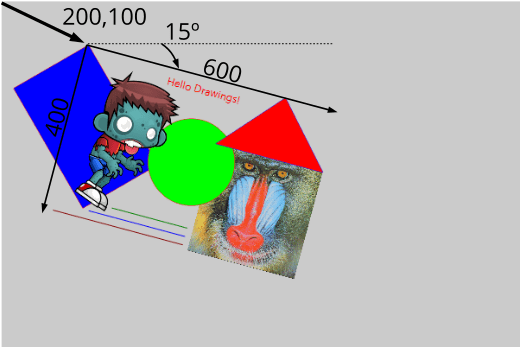
1.1. Sistemas cartesianos
Existe una dicotomía al dibujar en 2D: Por un lado, tradicionalmente los sistemas de escritorio y las imágenes digitales sitúan el origen de coordenadas en la esquina superior izquierda con el eje Y creciendo hacia abajo (Figura 10). Por otro lado, los sistemas cartesianos utilizados en geometría lo sitúan en la esquina inferior izquierda, con Y creciendo hacia arriba. Esto genera un dilema sobre si un sistema es mejor que otro.
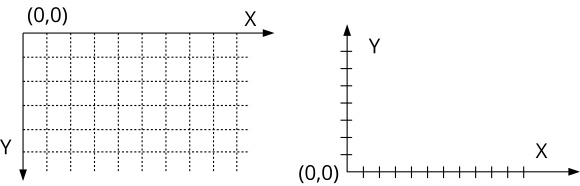
La respuesta es claramente no. Incluso, en el mismo dibujo, es posible que necesitemos combinar ambos en función del elemento que estemos tratando. Para textos e imágenes, el sistema de pantalla es más intuitivo ya que reproduce el papel o lienzo del mundo físico. Para funciones matemáticas, gráficos de barras, planos y otros aspectos relacionados con el mundo técnico, el cartesiano resulta mucho más cómodo y natural.
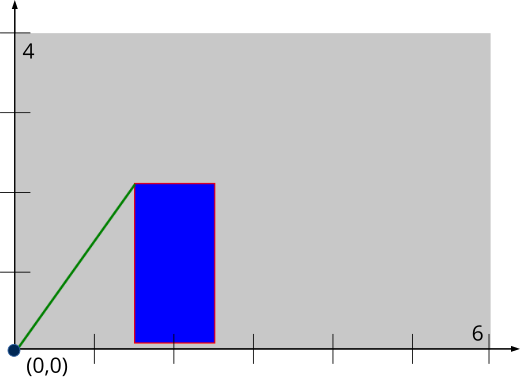
- draw_matrix_cartesianf establece el sistema de referencia del contexto en coordenadas cartesianas. En (Figura 11) hemos utilizado un sistema cartesiano de 6x4 unidades mapeado sobre una ventana de 600x400 píxeles.
1 2 3 4 5 6 7 8 9 |
T2Df t2d; draw_line_color(ctx, color_rgb(255, 0, 0)); draw_line_width(ctx, .03); draw_fill_color(ctx, color_rgb(0, 0, 255)); t2d_scalef(&t2d, kT2D_IDENTf, 100, 100); draw_matrix_cartesianf(ctx, &t2d); draw_rect(ctx, ekSKFILL, 1.5f, .1f, 1, 2); draw_line_color(ctx, color_rgb(0, 128, 0)); draw_line(ctx, 0, 0, 1.5f, 2.1f); |
2. Antialiasing
Dada la naturaleza discreta de los monitores e imágenes digitales, se produce un efecto de escalonado (dientes de sierra) al transformar las primitivas vectoriales a píxeles (Figura 12). Este efecto se hace menos perceptible a medida que aumenta la resolución de la imagen, pero aún así el "pixelado" sigue estando patente. El antialiasing, es una técnica que reduce este efecto de escalón variando ligeramente los colores de los píxeles en el entorno cercano a las líneas y contornos (Figura 13). Con esto se consigue engañar al ojo humano difuminando los bordes y generando imágenes de mayor calidad visual. Como contrapartida tenemos el coste en el rendimiento de aplicarlo, aunque hace años que los cálculos relativos al antialiasing se realizan directamente en hardware (Figura 14), por lo que el impacto será mínimo.
- draw_antialias permite activar o desactivar los cálculos del antialiasing.



3. Pantallas retina
Al final del 2014 Apple presentó su nueva línea iMac con Retina Display de alta resolución (5120x2880). Normalmente, estos monitores trabajan en modo escalado (2560x1440) lo que permite tener píxeles de doble densidad (Figura 15). Apple diferencia entre puntos en pantalla, que son los que realmente manipula la aplicación y los píxeles físicos. Por lo tanto, nuestra ventana de 600x400 realmente tendrá 1200x800 píxeles en ordenadores Retina, aunque la aplicación seguirá "viendo" solo 600x400 puntos. El sistema operativo realiza la conversión de forma transparente. De hecho, no tenemos que hacer nada para adaptar nuestro código, ya que funcionará de la misma forma tanto en iMac normales como en los equipados con monitores Retina.
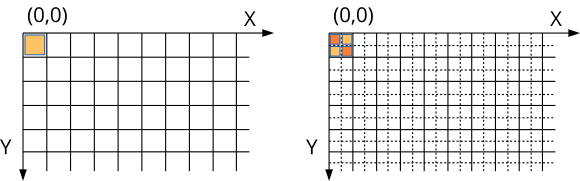
Esta doble densidad la aprovechará el rasterizador para generar imágenes de mayor calidad al disponer de más píxeles en el mismo área de pantalla. En (Figura 16) y (Figura 17) vemos la calidad extra que aportan estos modelos de monitor.


dctx_bitmap ()
Crea un contexto en memoria, con el fin de generar una imagen.
DCtx* dctx_bitmap(const uint32_t width, const uint32_t height, const pixformat_t format);
| width | Ancho de la imagen en píxeles. |
| height | Alto de la imagen en píxeles. |
| format | Formato de píxel de la imagen generada. |
Retorna
El contexto de dibujo.
Observaciones
Al terminar de dibujar, debemos llamar a dctx_image para obtener la imagen.
dctx_image ()
Obtiene la imagen resultado tras dibujar en el contexto creado con dctx_bitmap.
Image* dctx_image(DCtx **ctx);
| ctx | El contexto, que será destruido tras generar la imagen. |
Retorna
La imagen.
draw_clear ()
Borra todo el área del contexto, utilizando un color plano.
void draw_clear(DCtx *ctx, const color_t color);
| ctx | Contexto de dibujo. |
| color | Color de fondo. |
draw_matrix ()
Establece el sistema de referencia del contexto (transformación afín).
void draw_matrixf(DCtx *ctx, const T2Df *t2d); void draw_matrixd(DCtx *ctx, const T2Dd *t2d); void Draw::matrix(DCtx *ctx, const T2D *t2d);
| ctx | Contexto de dibujo. |
| t2d | Transformación. |
Observaciones
El origen de coordenadas está en la esquina superior izquierda. El eje Y aumenta hacia abajo.
draw_matrix_cartesian ()
Establece el sistema de referencia en coordenadas cartesianas.
void draw_matrix_cartesianf(DCtx *ctx, const T2Df *t2d); void draw_matrix_cartesiand(DCtx *ctx, const T2Dd *t2d); void Draw::matrix_cartesian(DCtx *ctx, const T2D *t2d);
| ctx | Contexto de dibujo. |
| t2d | Transformación. |
Observaciones
El origen de coordenadas está en la esquina inferior izquierda. El eje Y aumenta hacia arriba. Ver Sistemas cartesianos.
draw_antialias ()
Activa o desactiva el antialiasing.
void draw_antialias(DCtx *ctx, const bool_t on);
| ctx | Contexto de dibujo. |
| on |
|
Observaciones
El antialias puede cambiar en cada primitiva. No es necesario establecer una política para todo el dibujo. Ver Antialiasing.


