Binary search trees
This page has been automatically translated using the Google Translate API services. We are working on improving texts. Thank you for your understanding and patience.
Data container where the elements are stored in the form of a binary tree, optimizing searches, insertions or deletions. For sets of pointers consult Binary search trees (pointers) .
Functions
| SetSt(type)* | setst_create (...) |
| void | setst_destroy (...) |
| uint32_t | setst_size (...) |
| type* | setst_get (...) |
| const type* | setst_get_const (...) |
| type* | setst_insert (...) |
| bool_t | setst_delete (...) |
| type* | setst_first (...) |
| const type* | setst_first_const (...) |
| type* | setst_last (...) |
| const type* | setst_last_const (...) |
| type* | setst_next (...) |
| const type* | setst_next_const (...) |
| type* | setst_prev (...) |
| const type* | setst_prev_const (...) |
| void | setst_foreach (...) |
| void | setst_foreach_const (...) |
| void | setst_fornext (...) |
| void | setst_fornext_const (...) |
| void | setst_forback (...) |
| void | setst_forback_const (...) |
| void | setst_forprev (...) |
| void | setst_forprev_const (...) |
Like arrays binary search trees (BST), also known as sets or maps, are containers that allow us to work with a collection of objects. The main difference with the first ones is that the elements are not stored linearly in contiguous positions of memory, but use a tree-shaped structure where each node has two descendants (Listing 1) (Figure 1).
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
typedef struct _product_t Product; struct _product_t { type_t type; String *code; String *description; Image *image64; real32_t price; }; static int i_compare(const Product *p1, const Product *p2) { return str_scmp(p1->code, p2->code); } ArrSt(Product) *arrst = arrst_create(Product); ArrPt(Product) *arrpt = arrpt_create(Product); SetSt(Product) *setst = setst_create(i_compare, Product); SetPt(Product) *setpt = setpt_create(i_compare, Product); |
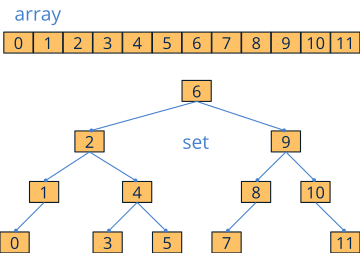
BSTs are structures optimized for cases where insertions, deletions and searches are very frequent. They are permanently sorted, hence it is possible to insert, delete or locate any element in logarithmic time O(logn), no need to use sort functions like arrst_sort (Figure 2). For maintenance to be carried out efficiently, the tree that supports the structure must meet a number of characteristics:
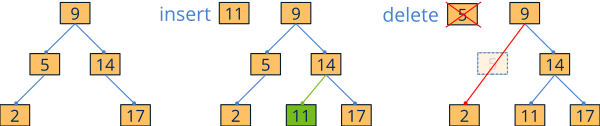
- Binary : Each node can only have 0, 1 or 2 children.
- Sorted : All descendants to the left of a node are of lesser value and those to the right of greater value. The order and search criteria are set in the constructor by a comparison function (
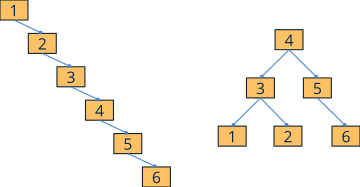
i_comparein the previous example) and cannot be changed during the lifetime of the container. The new elements will be inserted in their correct position according to this order. It does not support duplicate elements or in arbitrary positions. - Balanced: A tree can fulfill the two previous properties, but have degenerated to a list where searches can no longer be resolved in logarithmic time (Figure 3). Internally, the NAppGUI
Setcontainers are implemented with the so called red-black trees, where a maximum height of2log(n+1)is guaranteed. This is achieved by restructuring the tree after each insertion or deletion, so adding a new element (or removing it) is resolved in a maximum ofO(logn). This is much faster than in arrays, where have to move all the elements to insert a record in a specific position, with an associated cost ofO(n).
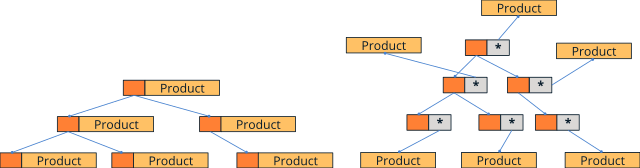
As we saw in Registers or pointers, we have two modalities when creating sets (Figure 4). The register-based version is more efficient than the pointer-based version, although less flexible.
- Use setst_create to create a set of registers.
- Use setpt_create to create a set of pointers.
1. Iterators
We cannot access the elements of a set using a random index, as was the case with arrays. The nodes are dispersed in different memory areas, which prevents calculating the position of a particular element from a base address. An iterator is nothing more than a pointer within the set that acts as a marker for the currently selected element (Figure 5). From a specific position, we can move to the previous or subsequent element, but never make arbitrary jumps. We can control the position of the iterator with different functions (Listing 2):
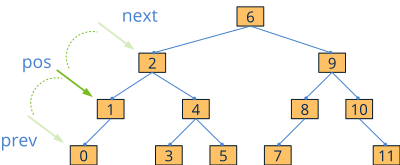
- Use setst_get to search for an item. The iterator will be fixed on it.
- Use setst_next to move the iterator to the next item.
- Use setst_prev to move the iterator to the previous item.
- Use setst_first to move the iterator to the first element of the set.
- Use setst_last to move the iterator to the last element of the set.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
const Product *product = setst_first(setst, Product); while (product != NULL) { // Do something ... product = setst_next(setst, Product); } setst_foreach(product, setst, Product) // Do something ... setst_fornext(product, setst, Product) // In reverse order setst_forback(product, setst, Product) // Do something ... setst_forprev(product, setst, Product) |
2. Arrays vs Sets comparative
We have performed a test to see the behavior of these two types of structures in real situations, apart from mere theory (Table 1). The structure used has been Product described in (Listing 1). We will compare six types of containers ArrSt(Product) and ArrPt(Product) (unsorted), ArrSt(Product) and ArrPt(Product) (sorted), SetSt(Product) and SetPt(Product).
- The items will be sorted by
codefield using the methodi_comparedescribed in (Listing 1). - The elements have been created previously and reside in memory. Times only reflect the management performed by the containers.
- Field
codetake values from"0"until"n-1", wheren=100,000is the number of elements. The elements have been previously messed up using the function bmem_shuffle_n. - The tests have been performed on a Raspberry Pi 3 Model B with NAppGUI compiled in Release version (Configurations). We have chosen this platform because of its clear technical inferiority with respect to others. In this way the asymptotic difference is more evident.
| Operation | ArrSt | ArrPt | ArrSt-Sort | ArrPt-Sort | SetSt | SetPt |
| Add(100k) | 0.006 | 0.004 | 27.600 | 2.896 | 0.159 | 0.274 |
| Loop(100k) | 0.000 | 0.000 | 0.000 | 0.000 | 0.022 | 0.025 |
| Search(100k) | 84.139 | 588.080 | 0.101 | 0.218 | 0.121 | 0.232 |
| Sort(100k) | 0.085 | 0.205 | - | - | - | - |
| Delete(100k) | 0.004 | 0.003 | 31.198 | 3.064 | 0.171 | 0.253 |
In view of these data, we can reach the following conclusions:
- Linear searches
O(n)are tremendously slow. - Keeping an array sorted after each insertion or deletion is expensive. It is more efficient to add all the elements and then order, although this will not always be possible. If the elements enter or leave arbitrarily but the set must always be ordered, it is better to use Sets.
- Register-based containers are more efficient in queries, but less when inserting or deleting. However, this test does not include the time to create or release dynamic memory, something inherent in pointer containers.
- Iterating in arrays is almost free, but iterating in sets has a small cost due to the logic of jumping between nodes.
- We cannot say that one container is better than another in general. It will depend on each specific case.
- For small groups (less than 1000 elements) the differences are practically imperceptible.
- For extremely small groups (up to 100 items) always use arrays. The asymptotic Sets improvement is marred by the much more efficient implementation of the Arrays.
setst_create ()
Create an empty set of registers.
SetSt(type)* setst_create(FPtr_compare func_compare, type);
| func_compare | Function to compare two elements. Sort and search. |
| type | Object type. |
Return
The new set.
setst_destroy ()
Destroy a set and all its elements.
void setst_destroy(SetSt(type) **set, FPtr_remove func_remove, type);
| set | The set. Will be set to |
| func_remove | Function that must free the memory associated with the object's fields, but not the object itself Destructors. If it is |
| type | Object type. |
setst_size ()
Get the number of set elements.
uint32_t setst_size(const SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Number of items.
setst_get ()
Search for an item in O(logn). It is equivalent to arrst_bsearch. If exists, the internal structure iterator will be fixed in it.
type* setst_get(SetSt(type) *set, const type *key, type);
1 2 3 4 |
Product key;
Product *pr;
key.id = 453;
pr = setst_get(setst, &key, Product);
|
| set | The set. |
| key | Search key. It is a pointer to an object where only the relevant search fields must be initialized. |
| type | Object type. |
Return
Pointer to the item if it exists, or NULL if not.
Remarks
setst_get_const ()
Const version of setst_get.
const type* setst_get_const(const SetSt(type) *set, const type *key, type);
| set | The set. |
| key | Search key. |
| type | Object type. |
Return
Element.
setst_insert ()
Insert a new item in the set.
type* setst_insert(SetSt(type) *set, type *key, type);
1 2 3 4 5 6 7 8 |
Product *pr; Product key; key.id = 345; pr = setst_insert(setst, &key, Product); if (pr != NULL) i_init(pr, 345, 100.45f); else error("Already exists"); |
| set | The set. |
| key | Key to insert. It is a pointer to an object where only the relevant search fields must be initialized. |
| type | Object type. |
Return
Pointer to the inserted element, which should be used to initialize the object. If an item with the same key already exists, it returns NULL.
Remarks
Inserting or deleting elements invalidates the internal set iterator Iterators. You must re-initialize it with setst_first.
setst_delete ()
Remove an item from the set.
bool_t setst_delete(SetSt(type) *set, type *key, FPtr_remove func_remove, type);
1 2 3 4 |
Product key; key.id = 345; if (setst_delete(setst, &key, product_remove, Product) == FALSE) error("Doesn't exists"); |
| set | The set. |
| key | Key to delete. It is a pointer to an object where only the relevant search fields must be initialized. |
| func_remove | Remove function. See setst_destroy. |
| type | Object type. |
Return
TRUE if the item has been deleted, or FALSE if there is no item with that key.
Remarks
Inserting or deleting elements invalidates the internal set iterator Iterators. You must re-initialize it with setst_first.
setst_first ()
Get the first set element and initialize the internal iterator.
type* setst_first(SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Pointer to the first element or NULL if the set is empty.
Remarks
setst_first_const ()
Const version of setst_first.
const type* setst_first_const(const SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Element.
setst_last ()
Get the last element of the set and initialize the internal iterator.
type* setst_last(SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Pointer to the last item or NULL if the set is empty.
Remarks
setst_last_const ()
Const version of setst_last.
const type* setst_last_const(const SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Element.
setst_next ()
Get the next set item, after increasing the internal iterator.
type* setst_next(SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Pointer to the next item or NULL if the iterator has reached the last.
Remarks
Use setst_first to initialize the internal iterator Iterators.
setst_next_const ()
Const version of setst_next.
const type* setst_next_const(const SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Element.
setst_prev ()
Gets the previous element of the set, after decrementing the internal iterator.
type* setst_prev(SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Pointer to the previous item or NULL if the iterator has reached the first.
Remarks
Use setst_last to initialize the internal iterator on reversed loops Iterators.
setst_prev_const ()
Const version of setst_prev.
const type* setst_prev_const(const SetSt(type) *set, type);
| set | The set. |
| type | Object type. |
Return
Element.
setst_foreach ()
Go through all the elements of the set. Use setst_fornext to close the loop.
void setst_foreach(type *elem, SetSt(type) *set, type);
1 2 3 |
setst_foreach(product, set, Product) bstd_printf("Position:%d, Id:%d\n", product_i, product->id); setst_fornext(product, set, Product) |
| elem | Name of the variable 'element' within the loop. Adding the suffix |
| set | The set. |
| type | Object type. |
setst_foreach_const ()
Const version of setst_foreach.
void setst_foreach_const(const type *elem, const SetSt(type) *set, type);
| elem | Element. |
| set | The set. |
| type | Object type. |
setst_fornext ()
Close the loop opened by setst_foreach, increasing the internal iterator.
void setst_fornext(type *elem, SetSt(type) *set, type);
| elem | Name of the variable 'element'. It must be the same as |
| set | The set. |
| type | Object type. |
setst_fornext_const ()
Const version of setst_fornext.
void setst_fornext_const(const type *elem, const SetSt(type) *set, type);
| elem | Element. |
| set | The set. |
| type | Object type. |
setst_forback ()
Go through all the elements of the set in reverse order. Use setst_forprev to close the loop.
void setst_forback(type *elem, SetSt(type) *set, type);
1 2 3 4 |
// Now in reverse order setst_forback(product, set, Product) bstd_printf("Position:%d, Id:%d\n", product_i, product->id); setst_forprev(product, set, Product) |
| elem | Name of the variable 'element' within the loop. Adding the suffix |
| set | The set. |
| type | Object type. |
setst_forback_const ()
Const version of setst_forback.
void setst_forback_const(const type *elem, const SetSt(type) *set, type);
| elem | Element. |
| set | The set. |
| type | Object type. |
setst_forprev ()
Close the loop opened by setst_forback, decreasing the internal iterator.
void setst_forprev(type *elem, SetSt(type) *set, type);
| elem | Name of the variable 'element'. It must be the same as |
| set | The set. |
| type | Object type. |
setst_forprev_const ()
Const version of setst_forprev.
void setst_forprev_const(const type *elem, const SetSt(type) *set, type);
| elem | Element. |
| set | The set. |
| type | Object type. |


